Physik-Denksport ist eigentlich anschauliches physikalisches Denken - nicht formelfixiert, sondern auf inneres Verständnis physikalischer Zusammenhänge zielend. Es geht also nicht primär um Berechnungen. Im Alltag begegnen uns viele Dinge, die bei genauerem Nachdenken gar nicht so einfach zu erklären sind. Natürlich kann uns ein Physiker eine Formel an den Kopf schmeissen - und die Sache hat sich. Ein inneres Verständnis des Phänomens gewinnen wir dadurch jedoch nicht.
Hier einige solche Fragen:
- Warum treffen ungleich schwere Gegenstände, die aus gleicher Höhe fallen gelassen werden, gleichzeitig auf dem Boden auf (wenn der Luftwiderstand keine Rolle spielt) ?
- Warum lässt eine verengende Düse am Gartenschlauch das Wasser weiter spritzen?
- Wie hoch muss ein Wandspiegel sein, damit man sich in ihm gerade von Kopf bis Fuss sieht?
- Warum erreicht uns Sonnenwärme durchs Vakuum des Weltalls hindurch?
Wer nur Formeln büffelt, hat damit die inneren Zusammenhänge noch nicht verstanden und wird eventuell beim Erklären "einfacher" Alltagserscheinungen kläglich scheitern.
Ein hervorragendes Buch ist hier unbedingt zu nennen und zu empfehlen:
Lewis C. Epstein, Epsteins Physikstunde, Birkhäuser, Basel, Boston, Berlin, 1989 / 1992

Vom gleichen Verfasser:
Lewis C. Epstein, Relativitätstheorie anschaulich dargestellt, Birkhäuser, Basel, Boston, Berlin, 1988
Aufgabe 1: Boot und Stein
In einem kleinen Teich schwimmt ein kleines Schalenboot, in dem sich ein Stein befindet. Jetzt wirft man den Stein aus dem Boot in den Teich. Was passiert mit dem Wasserpegel? Mögliche Antworten:
a) Der Wasserpegel steigt.
b) Der Wasserpegel sinkt.
c) Der Wasserpegel bleibt gleich.

Quelle: http://en.wikipedia.org/wiki/Traditional_fishing_boat#mediaviewer/File:Coracles_River_Teifi.jpg
Hinweis: Man übertreibe die Aufgabe: Der Stein ist im Vergleich zum Boot klein und schwer. Man denke sich den Stein nun sehr, sehr klein und sehr, sehr schwer...
Aufgabe 2: Ballspiel auf dem Karussell

Das Karussell dreht sich in Pfeilrichtung.
Aussen steht Person A, innen Person B.
Fig a): A wirft oder rollt B einen Ball zu. A zielt genau in Richtung von B.
Was trifft zu?
a) Der Ball trifft genau bei B ein.
b) Der Ball fliegt oder rollt von A aus gesehen links an B vorbei.
c) Der Ball fliegt oder rollt von A aus gesehen rechts an B vorbei.
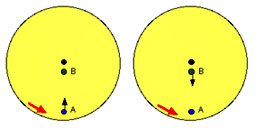
Fig. a) Fig. b)
Fig b): Nun hat B einen Ball in der Hand und rollt ihn genau in die Richtung von A. Was passiert?
a) Der Ball trifft genau bei A ein.
b) Der Ball rollt von B aus gesehen links an A vorbei.
c) Der Ball rollt von B aus gesehen rechts an A vorbei.
Quellen:
Epsteins Physikstunde
Temporär installierter Versuch im Technorama Winterhur
Aufgabe 3: Der geheimnisvolle Koffer
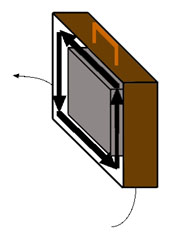
Hier sieht man durch die linke Kofferwand ins Innere eines Koffers mit einem seltsamen Innenleben *. Ein solcher Koffer war einst im Technorama Winterthur auszuprobieren.
Im Innern des Koffers rotiert -angetrieben durch eine im Mittelklotz versteckte Pumpe- eine Flüssigkeit in Pfeilrichtung im Kreis herum. Im Technorama war es ein Schwungrad.
Trägt man den Koffer geradeaus, merkt man nicht viel von diesem Innenleben; man spürt einfach das Gewicht des Koffers und der Flüssigkeit.
Was aber passiert, wenn wir mit diesem Koffer in der Hand eine Linkskurve gehen?
*) Die geniale Idee mit dem Flüssigkeitsstrom stammt von L.C.Epstein: Epsteins Physikstunde
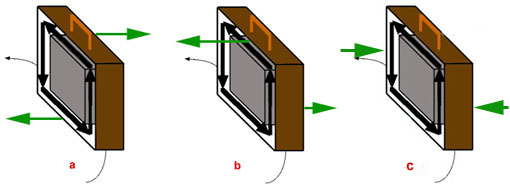
Welche Antwort ist richtig?
a) Der Koffer kippt wie im Bild a) "aus der Kurve heraus".
b) Der Koffer kippt wie in Bild b) "in die Kurve hinein".
c) Der Koffer widersetzt sich der Drehung wie im Bild c.
d) Der Koffer dreht sich einfach ganz normal um die Ecke.
Links:
Uni Göttingen
http://de.wikipedia.org/wiki/Pr%C3%A4zession
Aufgabe 4: Eintauchen
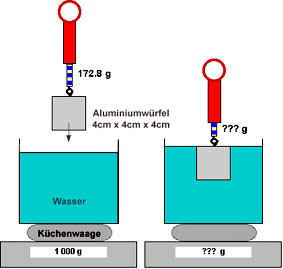
Ein Aluminiumwürfel mit Kantenlänge 4 cm hängt an einer Federwaage, die mit einer "Gramm-Skala" versehen ist*. Die Federwaage zeigt 172.8 g an. Auf einer Küchenwaage steht ein Becken mit Wasser. Die Küchenwaage zeigt genau 1000 g an. Nun wird der Aluwürfel an der Federwaage in Wasser eingetaucht. Was zeigen nun Federwaage und Küchenwaage an?
Die Federwaage zeigt...
Die Küchenwaage zeigt...
* Eigentlich zeigt eine Federwaage ja ein Gewicht, d.h. eine Kraft, an (im Beispiel obigen Aluwürfels ca. 1.7 N). Für Alltagszwecke sind viele "Waagen" - wie auch Küchenwaagen - "umgeeicht" in Masse-Einheiten.
Aufgabe 5: Elektromagnet
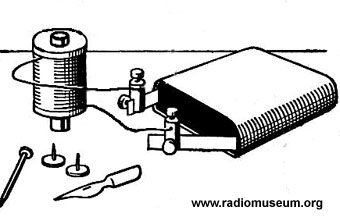
Das Bild zeigt einen Elektromagneten: In einer Drahtspule befindet sich ein Eisenzylinder. Schaltet man den Strom ein, wird der Eisenzylinder magnetisch. Unterbricht man den Strom, verschwindet die Magnetwirkung wieder.
Herr Schlaumeier überlegt nun folgendes:
"Strom macht also das Eisen zu einem Magneten. Dann kann ich die Sache doch auch umkehren:
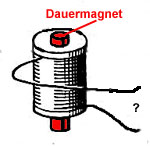
Wenn in der Spule ein richtiger Dauermagnet liegt (rot), müsste dann nicht Strom durch die Drähte fliessen?"
Was trifft zu?
a) Herr Schlaumeier hat recht.
b) Herr Schlaumeier hat nicht recht.
Aufgabe 6: Elektromotor-Bremse

Als die ersten Elektrolokomotiven durch die Alpen fuhren, wurde vorgeschlagen, dass diese Lokomotiven auf langen Gefällstrecken wie folgt bremsen sollten:
Man trennt den Elektromotor von der Zuleitung ab und schliesst ihn stattdessen an einen grossen Drahtwiderstand an, z.B. an eine grosse Spule aus Eisendraht. Der Motor dreht sich wegen des Gefälles und produziert deshalb Energie, d.h. er wirkt wie ein Dynamo. Mit diesem Strom heizt er den Drahtwiderstand auf: Wärme verpufft. Die Motoren-Energie wird also in Wärme umgewandelt, der Motor verliert Energie und bremst somit ab.
Geht dies tatsächlich?
a) ja
b) nein
Aufgabe 7: Elektromotor
In der Lösung zu Aufgabe 5 ("Elektromagnet") wird erklärt, dass Strom entsteht, wenn ein Permanent-Magnet in einer Spule (oder eine Spule in einem Magnetfeld) bewegt wird.
Auch ein Elektromotor besteht aus Drahtspulen, die sich in einem Magnetfeld drehen, wenn Strom durch die Spulen fliesst.
Wenn man nun umgekehrt den Elektromotor von Hand (oder durch einen andern mechanischen Antrieb) dreht, wird in den Drähten des Motors Strom erzeugt: Man hat einen Stromgenerator, einen Dynamo.
Herr Schlaumeier überlegt nun so:
"Ein Elektromotor, den ich von Hand antreibe, wirkt also als Stromerzeuger, als Generator. - Einem Elektromotor ist aber doch egal, wodurch er angetrieben wird: Dreht sich der Rotor, wird einfach Strom erzeugt.
Wenn ich nun also den Elektromotor an eine Stromquelle anschliesse, beginnt er zu laufen und damit verbraucht er nicht nur elektrische Energie, sondern er erzeugt gleichzeitig auch elektrische Energie."
a) Herr Schlaumeiers Überlegung ist richtig.
b) Herr Schlaumeier hat irgendwo einen Denkfehler gemacht; ein Motor kann nicht gleichzeitig elektrische Energie brauchen und erzeugen.
Quelle: Epsteins Physikstunde (s. Quellenangabe am Anfang)
Aufgabe 8: Fadenspule
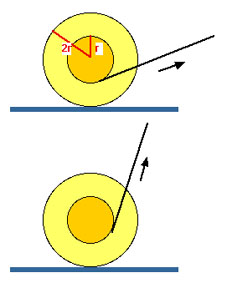
Eine Spule, auf der Faden oder dünner Draht aufgewickelt ist, hat einen inneren Kern mit Radius r und zwei äussere Scheiben mit Radius 2r.
Man zieht einmal sehr flach (Bild oben) und einmal sehr steil (Bild unten) am Faden.
Welche der folgenden Aussagen trifft zu?
Oberes Bild:
a) Die Spule rollt zur ziehenden Person hin.
b) Die Spule rollt von der ziehenden Person weg.
Unteres Bild:
a) Die Spule rollt zur ziehenden Person hin.
b) Die Spule rollt von der ziehenden Person weg.
Quellen:
Diese Fadenspulaufgabe erscheint in verschiedensten Physiklehrgängen und -vorlesungen. Sie erscheint z.B. auch in:
Norbert Treitz, Spiele mit Physik, Verlag Harri Deutsch, Thun, Frankfurt a.M. 1983, ISBN 3-87144-632-7.
Aufgabe 9: Fallende Körper 1
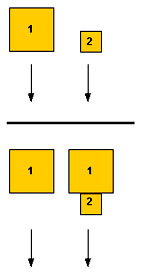
Ein grosser und ein kleiner Quader aus gleichem Material fallen in die Tiefe (Bild links, obere Reihe). Wenn man vom Luftwiderstand absieht:
Welche der folgenden Aussagen trifft zu:
a) Der schwerere Körper trifft früher auf dem Boden auf als der leichtere.
b) Der leichtere Körper trifft früher auf.
c) Beide treffen gleichzeitig auf.
Und wie steht es mit den Körpern der unteren Reihe der Illustration?
a) Die Kombination 1+2 rechts trifft später auf dem Boden auf als der Körper 1 (links) allein.
b) Die Kombination 1+2 trifft früher unten auf als Körper 1 allein.
c) Beide treffen gleichzeitig auf.
Quelle: Ernst Mach: Die Mechanik in ihrer Entwicklung. ISBN 3-534-05873-9
Aufgabe 10: Fallende Körper 2
![]()
Beim Lösen dieser Aufgabe ist kein physikalisches Formelwissen nötig. Geschicktes gedankliches Verknüpfen von Alltagserfahrungen genügt.
1. Frage:
Zwei Kugeln oder Steine werden gleichzeitig von einem Turm aus fallen gelassen. Der eine Stein startet allerdings 1 m höher als der andere (s. Bild). Was trifft zu?
a) Der Abstand zwischen den Kugeln bleibt während des Fallens unverändert.
b) Der Abstand zwischen den Kugeln vergrössert sich.
c) Der Abstand zwischen den Kugeln verringert sich.
2. Frage, etwas schwieriger:
Nehmen wir an, die beiden Kugeln wurden aus 20 m bzw. 21 m Höhe gleichzeitig fallen gelassen. Die obere Kugel schlägt einen kurzen Moment nach der unteren Kugel auf dem Boden auf.
Wenn wir jetzt den ganzen Versuch auf einen höheren Turm verlegen (Kugeln wieder mit 1 m Höhenunterschied gleichzeitig fallen gelassen), was trifft dann zu?
a) Die Zeitspanne zwischen dem Aufschlagen der beiden Kugeln bleibt gleich wie auf dem tieferen Turm.
b) Die Zeitspanne wird kürzer.
c) Die Zeitspanne wird länger.
3. Frage:
Wieder werden zwei Steine oder Kugeln von einem Turm aus fallen gelassen. Diesmal starten die Kugeln vom gleichen Ort aus, aber die zweite Kugel startet 0.5 s nach der ersten. Was trifft jetzt zu?
a) Der Abstand zwischen den Kugeln bleibt stets gleich.
b) Der Abstand vergrössert sich zunehmend.
4. Frage:
Die zweite Kugel starte 0.5 s nach der ersten Kugel. Wie viel Zeit nach der ersten Kugel wird die zweite Kugel auf dem Boden aufschlagen?
a) Die zweite Kugel schlägt 0.5 s nach der ersten auf dem Boden auf.
b) Die zweite Kugel schlägt mehr als eine halbe Sekunde nach der ersten auf.
c) Die zweite Kugel schlägt weniger als eine halbe Sekunde nach der ersten auf
Quelle: Epsteins Physikstunde
Aufgabe 11: Einwurf beim Fussball

Wird eine Kugel mit Hilfe einer mechanischen Vorrichtung schräg nach oben abgeschossen, so weiss man, dass bei einem Abflugwinkel von 45° schräg nach oben die Kugel am weitesten fliegt.
Was trifft wohl beim zweihändigen Einwurf im Fussball zu?
Der Winkel, der den Ball am weitesten fliegen lässt, ist
a) 45°.
b) steiler als 45°.
c) flacher als 45°.
Aufgabe 12: heiss und kalt
Versuch 1:
Man mischt 100 g siedendes Wasser (100° C) mit 100 g eiskaltem Wasser (0°C). Welche Mischtemperatur ist zu erwarten?
a) 25°
b) 50°
c) 75°
Versuch 2:
Man mischt 100 g Eis von 0°C mit 100 siedendem Wasser (100° C). Was trifft zu?
Die Mischtemperatur ist
a) die gleiche wie in Versuch 1.
b) höher als in Versuch 1.
c) tiefer als in Versuch 1.
Quelle: N. Treitz: Spiele mit Physik. Harri Deutsch, Thun, Frankfurt a.M. 1983.
Aufgabe 13: Holzstab balancieren

Man hat einen dünnen Holzstab oder einen Besenstiel. Wie kann man ohne zu messen die Mitte feststellen?
Die Antwort wird vermutlich nicht schwerfallen: Man balanciert den Stab auf einem dünnen Gegenstand, etwa einer Messerklinge und bestimmt so den Schwerpunkt.
Den Schwerpunkt erhält man auch durch folgende kleine Vorführung:
Man hält den Stab auf beiden Zeigefingern. Die Finger müssen überhaupt nicht gleich weit von der Mitte entfernt sein. Jetzt bewegt man die beiden Zeigefinger langsam und sorgfältig gegeneinander. Was passiert? - Ausprobieren.
Der Stab wird mal auf dem einen, mal auf dem andern Finger gleiten und auf dem jeweils andern Finger haften (Erklärung?). Gegen die Mitte hin wechselt dieses Spiel zwischen den Fingern immer schneller ab, und man landet auf jeden Fall beim Schwerpunkt.
Quellen:
- Diese Aufgabe erscheint in verschiedensten Physiklehrgängen und -vorlesungen.
- Sie erscheint auch in: Norbert Treitz, Spiele mit Physik, Verlag Deutsch, 1983
Frage 1:
Was trifft zu?
a) Das geht nur, weil beide Hände sich bewegen können.
b) Es geht auch, wenn eine Hand (mit ausgestrecktem Zeigefinger) auf einer Stuhllehne ruht. (Ausprobieren.)
Frage 2:
Was trifft zu?
a) Man kann mit diesem Vorgehen sogar den Schwerpunkt eines ganzen Besens (Stiel plus Borsten) bestimmen.
b) Nein, das geht nicht.
Frage 3:
Was trifft zu?
a) Das ganze geht auch, wenn man zwei Gummihandschuhe anzieht, welche die Reibung vergrössern.
b) Nein, dann geht es nicht mehr.
Frage 4:
Was trifft zu?
a) Es gelingt auch, wenn ich nur an einer Hand einen Gummihandschuh trage.
b) Nein, das geht nicht.
Aufgabe 14: Der berühmte Kletteraffe
Dieses Rätsel vom Kletteraffen erscheint in unzähligen Physikbüchern und -vorlesungen. Unsere Bildquelle: www.physik.uni-muenchen.de.
![]()
Affe und Gewicht sind gleich schwer.
Das Seil läuft oben über eine Rolle.
Der Affe in unserem Bild klettert in die Höhe. Was passiert mit dem Gewicht?
a) Es sinkt.
b) Es bleibt an Ort und Stelle.
c) Es steigt.
Aufgabe 15: Krafttraining

Arbeit oder nicht?
In manchen Physikbüchern liest man, dass physikalische Arbeit zum Beispiel bedeute, ein Gewicht um eine gewisse Höhe anzuheben (gegen die Erdanziehung). Manchmal wird dann noch ergänzt, dass das reine Halten eines Gewichtes keine Arbeit bedeute, denn das Gewicht bleibe ja am Ort und werde nicht angehoben.
Solche Situationen sind zum Beispiel folgende:
- Wir strecken einen Arm aus und jemand gibt uns eine Hantel in die Hand. Die halten wir jetzt ruhig nach aussen.
- Wir hängen mit gebeugten Armen an einer Reckstange.
- Wir stützen uns mit leicht gebeugten Armen in der Liegestützstellung auf, ohne uns zu bewegen.
Welche der folgenden Aussagen treffen zu?
a) In den vorgängig beschriebenen Situationen verrichte ich keine Arbeit, denn ich bewege mich ja überhaupt nicht.
b) Ich verrichte trotzdem Arbeit, denn ich merke ja, wie ich zunehmend erschöpft werde und ich beginne auch zu schwitzen.
c) Die Physik kann auf diese Situationen nicht angewendet werden.
Nach Richard Feynmann, Vorlesungen über Physik, 2. Band, Oldenburg-Verlag, 2001.
Aufgabe 16: Kreisbewegung
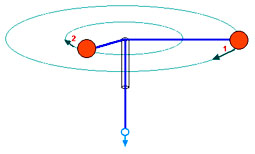
Abb. 1
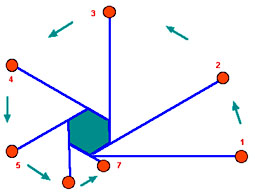
Abb. 2
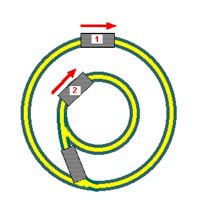
Abb. 3
Abb. 1: Eine Kugel ist an einer Schnur befestigt und wird im Kreis herumgeschwungen. Der Faden läuft in der MItte durch ein fest montiertes Röhrchen. Zieht man am hellblauen Ringlein unten, verkürzt sich die Schnur und die Kugel gerät von der Umlaufbahn 1 allmählich auf die engere Umlaufbahn 2.
Man zieht nun eine kurze Zeit am hellblauen Ringlein und verkürzt so den Faden. Was trifft für Position 2 zu?
a) Die Geschwindigkeit der Kugel hat sich in Position 2 erhöht.
b) Die Geschwindigkeit hat sich nicht verändert.
c) Die Geschwindigkeit hat sch verringert.
Abb 2: Die Kugel läuft wieder an einem Faden rundherum, diesmal ist der Faden an einem Pfosten mit sechseckigem Profil befestigt, wird am Pfosten aufgewickelt und daher immer kürzer. Die Kugel durchläuft die Positionen 1 bis 7. Was trifft beim Kreisen und Aufwickeln des Fadens zu?
a) Die Geschwindigkeit der Kugel vergrössert sich zusehends.
b) Die Geschwindigkeit ändert sich nicht.
c) Die Geschwindigkeit verringert sich.
Abb. 3: Dieses Beispiel stammt -leicht abgewandelt- nochmals aus dem Buch von L.C. Epstein ("Epsteins Physikstunde"):
Ein Luftkissenfahrzeug gleitet antriebslos, aber ohne Gleitwiderstand mit konstanter Geschwindigkeit auf der äusseren Kreisbahn 1.
Nun wird eine Weiche gestellt und das Fahrzeug gelangt in den inneren Kreis 2. Was trifft zu?
a) Die Fahrzeuggeschwindigkeit erhöht sich im inneren Kreis.
b) Die Fahrzeuggeschwindigkeit bleibt auch im inneren Kreis unverändert.
Aufgabe 17: Kräfte
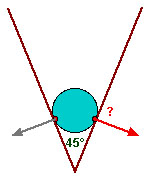
Eine schwere Metallkugel steckt in einem keilförmigen Spalt (Öffnungswinkel 45°). Die Kugel drückt dabei an den rot bezeichneten Punkten auf die Spaltwände und übt dabei eine Kraft auf diese Wände aus.
Betrachten wir die durch den roten Pfeil gekennzeichnete Kraft, welche die Kugel auf die rechte Wand ausübt.
Was trifft zu?
a) Diese Kraft ist kleiner als die Gewichtskraft der Kugel, da sich das Gewicht der Kugel ja auf zwei Aulagepunkte verteilt.
b) Diese Kraft ist exakt die Hälfte der Gewichtskraft der Kugel.
c) Diese Kraft ist gleich gross wie die Gewichtskraft der Kugel.
d) Diese Kraft ist grösser als die Gewichtskraft der Kugel.
Aufgabe 18: Möwenfüsse
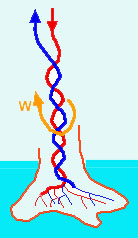
Das Bild zeigt schematisch einen Möwenfuss mit den Blutbahnen. Rot: zufliessendes Blut. Blau: zurückfliessendes Blut. Die Hauptblutbahnen in den Möwenbeinen, die das Blut in die Füsse (rot) und von den Füssen wieder zurück in den Körper (blau) führen, sind eng miteinander in Kontakt.
Welche Vorteile hat dies?
Welche Behauptung trifft zu?
a) Es hat mit der Stabilität zu tun.
b) Es ist ein Platzproblem in den dünnen Beinen.
c) Es verhindert allzu grossen Wärmeverlust beim Stehen auf Eis und gefrorenen Böden.
Aufgabe 19: Fallende und rollende Zylinder
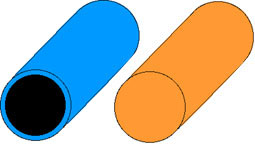
Das Bild zeigt links einen metallenen Hohlzylinder und rechts einen massiven Holzzylinder. Beide seien gleich schwer. Wir könnten uns beim Hohlzylinder noch zwei dünne Deckel denken, welche den Hohlraum unsichtbar machen. Beide Zylinder könnten gleich bemalt werden, so dass sie äusserlich nicht zu unterscheiden sind. Auch das Gewicht unterscheidet sie nicht.
Frage 1: Beide Zylinder werden aus gleicher Höhe gleichzeitig fallen gelassen. Was trifft zu?
a) Beide Zylinder treffen gleichzeitig auf dem Boden auf.
b) Der massive Holzzylinder trifft früher auf.
c) Der metallene Hohlzylinder trifft früher auf.
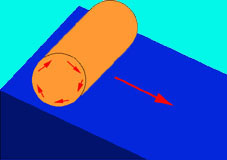
Frage 2: Nun lässt man beide Zylinder eine schiefe Ebene hinunterrollen. Was trifft zu?
a) Beide Zylinder rollen gleichzeitig über die Ziellinie am unteren Ende der schiefen Ebene.
b) Der Holzzylinder ist schneller am Ziel.
c) Der metallene Hohlzylinder ist schneller am Ziel.
Aufgabe 20: Zwei gleitende Körper
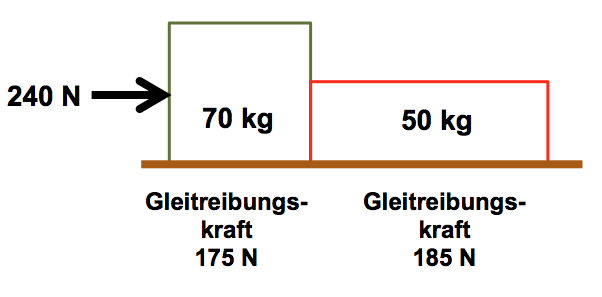
Zwei Blöcke bewegen sich auf waagrechter Unterlage nach rechts.
Auf Block 1 wirkt von links eine Kraft von 240 N.
Auf Block 1 wirkt eine Gleitreibungskraft von 175 N, auf Block 2 eine solche von 185 N.
Wie gross ist die Kraft vom linken Körper 1 auf den rechten Körper 2?
Eine Multiple-Choice-Auswahl:
a) 55 N
b) 135 N
c) 185 N
d) 235 N
Aufgabe 21: Schwimmen
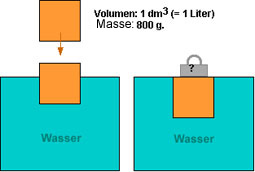
Ein Holzklotz mit einem Volumen von 1 Kubikdezimeter (= 1 Liter) "wiegt" 800g. Taucht man ihn in Wasser, schwimmt er.
Mit welchem Gewicht einer Marktwaage muss man den Klotz beschweren, damit er gerade vollständig unter die Wasseroberfläche taucht?
A: 50 g, B: 100 g, C: 200 g, D: 800 g, E: 1000 g.
Aufgabe 22: Waage
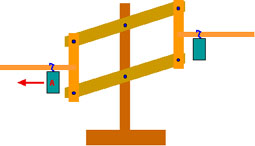
Die beiden blauen Gewichte sind gleich schwer. Wenn man bei dieser Waage das linke Gewicht (A) nach links verschiebt, dann
A: senkt sich die Waage nach links
B: bleibt die Waage im Gleichgewicht.
Was trifft zu?
Aufgabe 23: Wandspiegel
Wie hoch muss ein Wandspiegel sein, damit man sich in ihm gerade noch von Kopf bis Fuss sehen kann?
A: Gleich gross wie die Person
B:
Das kann man nicht sagen; es hängt von der Betrachtungsdistanz ab.
C: Halb so gross wie die Person.
D: Spiegelhöhe = 1/3 der Personengrösse.

August Macke: Spiegelbild im Schaufenster
Aufgabe 24: Wasser fliesst aus
Drei gleiche Zylindergefässe sind mit Wasser gefüllt. Knapp über dem Boden befindet sich ein Abflussloch.
Bild links: Das Loch wurde von aussen gebohrt und hat eine Metall-Braue im Inneren.
Bild Mitte: Das Loch ist ohne Braue sauber gebohrt und ganz scharfkantig.
Bild rechts: Das Loch ist innen gerundet.
Die Querschnittsflächen aller drei Ausgüsse sind bei der Austrittsstelle genau gleich gross.
Was trifft zu?
A: Alle drei Gefässe verlieren das Wasser gleich schnell.
B: Das Gefäss rechts verliert das Wasser am schnellsten, das mittlere am langsamsten.
C: Das Gefäss rechts
verliert das Wasser am schnellsten, das linke am langsamsten.
D: Das Gefäss in der Mitte verliert das Wasser am schnellsten.
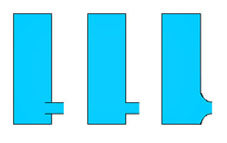
Quelle: Richard Feynmann, Vorlesungen über Physik, 2. Band, Oldenburg-Verlag, 2001.
Aufgabe 25: Wasserdruck
Die Bodenfläche ist bei allen 6 Gefässen gleich gross. Alle Gefässe sind gleich hoch mit Wasser gefüllt.
Was trifft zu?
A: Auf alle 6 Gefässböden wirkt die gleich grosse Kraft.
B: Bei a und b ist die Kraft auf den Boden gleich gross, bei den andern verschieden.
C: Bei 5 Gefässen ist die Bodenkraft gleich gross, bei e ist sie kleiner, da hier viel weniger Wasser im Spiel ist.
D: Bei jedem Gefäss ist die Kraft verschieden.

Aufgabe 26: Druck in einem Wasserkübel

Ein Zylindergefäss ist mit Wasser gefüllt. Beim Tauchen spüren wir, wie der Druck mit zunehmender Tiefe grösser wird. Hier sei der Druck betrachtet, den die Zylinderwände "spüren". Was trifft zu?
A: Bei beiden Punkten (A und B) ist der Wanddruck gleich gross.
B: Bei B ist der Wanddruck grösser als bei A.
Ein Anschlussrätsel:
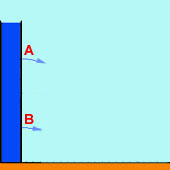
Ein 40 cm hohes Zylindergefäss steht direkt auf dem Boden und ist randvoll mit Wasser gefüllt.
Bei A und B seien kleine Löchlein in die Zylinderwand gebohrt. Das obere Loch A befinde sich z.B. 10 cm unterhalb der Wasserlinie, das untere Loch B befinde sich 10 cm über dem Gefässboden.
Durch die beiden Löchlein spritzt das Wasser heraus. Wir messen, wie weit der Strahl kommt, bis er auf dem Boden auftrifft.
Das auslaufende Wasser wird von oben laufend ersetzt.
Was trifft zu?
A: Strahl A kommt weiter als Strahl B.
B: Strahl B kommt weiter als Strahl A.
C: Bei Strahlen kommen gleich weit.
Aufgabe 27: Wasserschlacht am Brunnen

Fall A: Brunnenrohr direkt am Reservoir:
Ein grosses und hohes Gefäss (Wasserreservoir) ist mit Wasser gefüllt. Im unteren Teil befinden sich auf gleicher Höhe zwei Öffnungen, aus denen das Wasser herausspritzt. Bei einer der Öffnungen ist eine Düse montiert, die den Ausguss verengt. Die andere Öffnung wird nicht verengt. Was trifft zu?
A: Das Wasser durch die verengte Düsenöffnung fliesst mit stärkerem Druck heraus.
B: Das Wasser durch die normale Öffnung fliesst mit stärkerem Druck heraus.
C: Durch beide Öffungen fliesst das Wasser mit gleichem Druck heraus.
Fall B: Brunnen weit weg vom Reservoir

Die Antwort des Rätsels links (Brunnenhahn direkt am Reseervoir) erstaunt (s. Lösungen): Die Düse nützt dort gar nichts!
Wir wissen aber doch aus Erfahrung, dass wir durch Verengen einer Brunnenröhre oder durch eine Düse am Gartenschlauch den Wasserstrahl viel weiter spritzen lassen können als bei normaler Öffnung. Wie lautet denn hier die Erklärung? Was trifft zu?
A: Das erklärt sich dadurch, dass Wasser durch eine Verengung schneller fliesst als sonst.
B: Das erklärt sich mit Hilfe der Reibung des fliessenden Wassers in den Zuleitungen.
C: Das hat mit einem speziellen Mechanismus im Wasserwerk zu tun.
Aufgabe 28: Wettrennen
Adrian und Carla machen ein Wettrennen über 100 m. Carla gewinnt. Wie sie die 100m-Linie überquert, ist Adrian erst bei 95 m angelangt.
Da Adrian etwas jünger ist als Carla, wird beim zweiten Lauf für Carla eine Erschwerung eingebaut: Sie startet 5 m hinter der Startlinie, muss also 105m rennen, während Adrian bei der Startlinie losrennen darf.
Was trifft nun vermutlich zu?
A: Adrian wird jetzt gewinnen.
B: Beide werden die 100m-Llinie gleichzeitig passieren.
C: Carla wird immer noch gewinnen.
Aufgabe 29: Wärme
Frage 1:
Kommen ein warmer und ein kalter Körper miteinander in Kontakt, wird Wärmeenergie übertragen. Auch Gase, z.B. Luft, können Wärme weiterleiten. Wie steht es im luftleeren Raum des Weltalls? Was trifft zu?
A: Wärme wird auch durchs Vakuum des Weltalls weitergeleitet.
B: Wärme wird nur über direkten Kontakt von Materie weitergeleitet.
Frage 2:
Was schmilzt schneller
in der Sonne: Weisser, unverschmutzter Schnee oder eine gleiche Menge durch Russ verschmutzter, schwarz gefärbter Schnee?
A: Der weisse Schnee schmilzt in der Sonne schneller.
B: Der verschmutzte Schnee schmilzt schneller.
C: Beide schmelzen gleich schnell.
Frage 3:
Heller, unverschmutzter Schnee und dunkler, russverschmutzter Schnee werden in gleicher Menge je in einem Topf bei gleicher Wärmezufuhr erhitzt. Was trifft zu?
A: Der helle Schnee schmilzt schneller.
B: Der dunkle Schnee schmilzt schneller.
C: Beide schmelzen gleich schnell.
Frage 4:
Ein heller und ein dunkler Metallwürfel gleicher Grösse werden auf gleich hohe Temperatur erhitzt. Beide Körper werden in der Folge Wärmestrahlung aussenden. Was trifft zu?
A: Der helle Körper strahlt in der gleichen Zeit mehr Wärme ab als der dunkle.
B: Der dunkle strahlt mehr ab.
C: Bei strahlen gleich viel ab.
Frage 5:
Wird einem Stoff Wärme zugeführt, erwärmt sich dieser Stoff, d.h. seine Temperatur erhöht sich.
A: Das ist immer so.
B: Das ist nicht immer so.
Aufgabe 30: Zerreissprobe
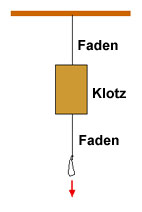
Man zieht am Fadenende nach unten. Wo reisst der Faden?
A: Oberhalb des Klotzes.
B: Unterhalb des Klotzes.
C: Das kommt drauf an, wie man zieht.
Aufgabe 31: Breite Spritze, schmale Spritze
Frage 1:
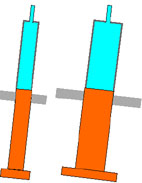
Nehmen wir an, wir drücken die Kolben der beiden Spritzen mit stets gleich grosser Kraft nach innen. Die Düsenspitzen beider Spritzen seien von gleicher Grösse. Was trifft zu?
A: Die schmale Spritze spritzt bei gleicher Kraftanwendung weiter.
B: Die breite Spritze spritzt weiter.
C: Beide spritzen gleich weit.
Frage 2:
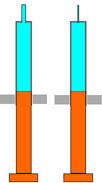
Wir drücken erneut mit stets gleich grosser Kraft. Was trifft zu?
A: Die Spritze links mit der breiten Düse spritzt weiter.
B: Die Spritze rechts mit der schmalen Düse spritzt weiter.
C: Beide spritzen gleich weit.
Aufgabe 32: Warum gibt es Koloratursopranistinnen, aber keine Koloraturbässe?


Links: Königin der Nacht aus Mozarts Zauberflöte (Koloratursopran), oben ein Notenausschnitt der berühmten Arie.
Warum könnte Sarastro eine Koloratur dieses Tempos in die Basslage versetzt nicht singen?
Aufgabe 33: Rollendes Trottoir
Kinder probieren auf Rolltreppen und rollenden Trottoirs -nicht immer zur Freude aller Erwachsenen- gerne aus, ob sie in beiden Richtungen gehen können.
Linda und Max probieren mithilfe eines rollenden Trottoirs in einer Metrostation folgendes aus:
Linda läuft mit der Eigengeschwindigkeit v auf dem Band von A nach B und anschliessend gleich wieder von B zurück nach A. Das Band rollt mit der Geschwindigkeit w.
Max läuft auf dem parallel zum Rollband verlaufenden normalen Korridor ebenfalls mit Geschwindigkeit v von A nach B und gleich wieder zurück von B nach A.
Was trifft zu?
A: Linda trifft zuerst wieder bei A ein.
B: Max trifft zuerst wieder bei A ein.
C: Beide treffen gleichzeitig wieder bei A ein.

Aufgabe 34: Tacho-Abstandsregel
Eine gängige Tacho-Abstandsregel für den Abstand des eigenen Autos zum vorausfahrenden Fahrzeug besagt:
Auf Schnellstrassen und Autobahnen: 1 Tachoabstand einhalten, d.h. so viele Meter Abstand halten wie der Tachometer km/h anzeigt.
Innerorts: halber Tachoabstand, d.h. halb so viele Meter Abstand wie der Tachometer km/h anzeigt.
Was trifft zu?
A: Diese Regel ist vernünftig.
B: Diese Regel ist zu knapp bemessen.

Aufgabe 35: Gleitendes Boot ("Stiefeln")
Ein Boot kann man mit dem Heckruder nur steuern, wenn es relativ zum Wasser schneller vorankommt als dieses. Kann man also ein antriebslos auf einem Fluss treibendes Boot steuern oder nicht?
A: ja, man kann
B: nein, man kann nicht

Aufgabe 37: Optimal bemessener Balken bezüglich Tragkraft
Die Tragkraft eines Balkens ist proportional zu d2b.
d = Dicke und b = Breite des Balkens.
Aus einem kreisrunden Stamm mit Durchmesser D=1 soll ein Rechteckbalken mit maximaler Tragkraft herausgesägt werden.
Unser Gefühl sagt uns, dass der Balken "hochkant" stabiler ist als z.B. ein Balken mit quadratischem Querschnitt (also d > b).

Wie ist das Verhältnis d : b zu bemessen?
Aufgabe 38a: Was vertauscht ein Spiegel eigentlich?
Oft wird gesagt, ein Spiegel vertausche links und rechts. Wie steht es dann aber, wenn ich auf einem Spiegelboden stehe? Vertauscht sich dann oben mit unten? Was wird nun eigentlich in einem Spiegel "vertauscht"?
Aufgabe 38b: Metalllöffel
Was passiert, wenn ich in die Innenseite eines metallenen Suppenlöffels blicke?
Aufgabe 39: Drehteller
Auf einem Drehteller mit Radius R und Winkelgeschwindigkeit ω verläuft eine Schiene durchs Drehzentrum. Ein (reibungsfrei rollender) Wagen wird von der Peripherie zum Zentrum gestossen.
Wie gross ist die mindestens aufzuwendende Arbeit und somit die potentielle Energie, die der Wagen bei seiner Ankunft im Zentrum gewonnen hat?
Lässt man den Wagen in Zentrumsnähe* wieder los, wird er sich in beschleunigter Fahrt Richtung Peripherie bewegen. Mit welcher Geschwindigkeit kommt er dort an?
*Liesse man den Wagen genau im Zentrum los, geschähe nichts.
Aufgabe 40: Drehteller 2: Film rückwärts (Zeitumkehr)
Jemand filmt den Vorgang von Aufgabe 39, bei welchem der Wagen aus Zentrumsnähe losgelassen wird und, sich beschleunigend, zur Peripherie bewegt. Der Beschleunigungsvektor zeigt dabei radial nach aussen.
Nun lässt man diesen Film rückwärts laufen (Zeitumkehr). Was geschieht im Rückwärtsfilm?
A: Der Beschleunigungsvektor zeigt jetzt nach innen zum Zentrum.
B: Der Beschleunigungsvektor zeigt immer noch nach aussen zur Peripherie.
Zusatzfrage:
Die Beschleunigung des Wagens auf dem Drehteller von Aufgabe 39 ist nicht konstant, sondern nimmt zu (d.h. die Beschleunigung ändert sich). Wie steht es, wenn man den Film wieder rückwärts laufen lässt mit der Beschleunigungsänderung?
A: Die Beschleunigungsänderung wird mit der Zeitumkehr ebenfalls umgekehrt.
B: Die Beschleunigungsänderung wird mit der Zeitumkehr nicht umgekehrt.
Aufgabe 41: Crash
Muskelprotz M mit Masse m findet es bei kurzen Fahrten im Auto nicht immer nötig, die Sicherheitsgurte zu benützen und fährt zudem noch ein uraltes Modell ohne Airbags. Da er intensiv Krafttraining betreibt, ist er überzeugt, eine allfällige Frontalkollision mit seinen starken Armen auffangen zu können.
Nehmen wir an, Herrn Ms Arme könnten eine Negativbeschleunigung von 4g stemmen. (Vergleich: Herr M lässt in Liegestützstellung noch 3 Personen seines Kalibers auf seinen Schultern reiten.)
Sei die "Knautschdistanz" s bei einer Kollision mit einer Mauer (oder bei einer Frontalkollision) etwa 0.5 m, und eine Negativbeschleunigung von 4g (ca. 40m/s2) soll nicht überschritten werden. Welche Fahrgeschwindigkeit erträgt es dann?
A: 11 km/h
B: 23 km/h
C: 42 km/h
D: 55 km/h
Aufgabe 42: Traktorräder
Starke Untersetzung bringt ein grosses Drehmoment T auf die Hinterrad-Antriebsachse eines Traktors. Welches ist der Vorteil grosser Hinterräder?

Aufgabe 43: Beschleunigungsrekord

Im Jahr 2016 beschleunigte der Elektrorennwagen "Grimsel" einer Gruppe der ETHZ und der Hochschule Luzern in 1.513 Sekunden von 0 auf 100 km/h.
Ein Problem bei zu rascher Beschleunigung ist das Überschreiten der maximal möglichen Haftreibung μ⋅M⋅g (μ=Haftreibungskoeffizient; M=Fahrzeugmasse; g=Erdbeschleunigung).
Macht man das Fahrzeug schwerer, erhöht sich die Haftreibung. Ist das die Lösung?
A: ja
B: nein
Aufgabe 44: Velospuren im Schnee
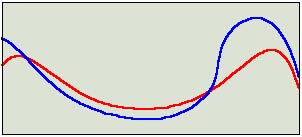
a) Welches ist die Vorderrad-, welches die Hinterradspur?
b) Fuhr das Velo von links nach rechts oder von rechts nach links?
Aufgabe 45: Senkrechte Kreisbewegung
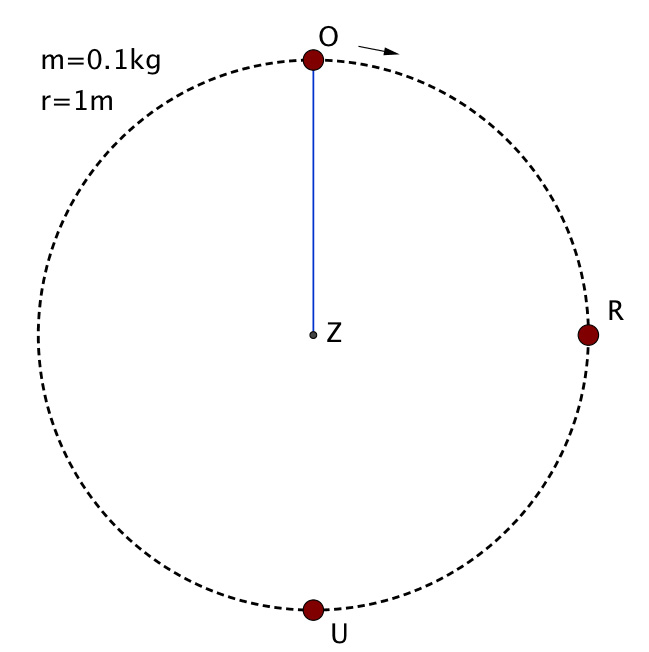
Man schwingt eine Masse von 0.1 kg, die an einem starken Faden von r=1m Länge befestigt ist senkrecht im Kreis herum. Den Faden denke man sich immer schön zentriert von Z aus geführt (was in der Praxis allerdings schwer zu bewerkstelligen ist). Reibung kann vernachlässigt werden.
a) Was trifft in Bezug auf die Fadenkraft F zu?
A: Die Fadenkraft bleibt konstant.
B: Die Fadenkraft ist oben am grössten und unten am kleinsten.
C: Die Fadenkraft ist oben am kleinsten und unten am grössten.
b) Was trifft in Bezug auf den Geschwindigkeitsbetrag (das Tempo) der Masse zu?
A: Das Tempo bleibt konstant.
B: Das Tempo ist oben am grössten und unten am kleinsten.
C: Das Tempo ist oben am kleinsten und unten am grössten.
c) Man dosiere nun den Schwung so, dass die Fadenkraft am höchsten Punkt gerade verschwindet. Wie gross sind bei O, R und U Geschwindigkeit, Zentripetalkraft und die ins Zentrum Z wirkende Fadenkraft?
Aufgabe 46: Schwerpunkt
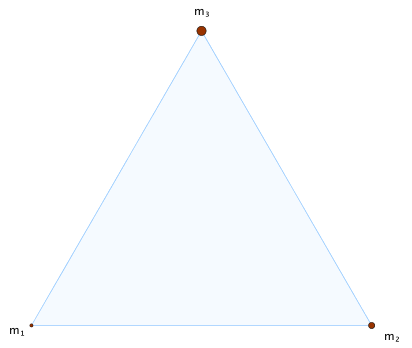
An den Eckpunkten eines sehr, sehr leichten (d.h. praktisch masselosen) gleichseitigen Dreiecks mit Seitenlänge 1 befinden sich Gewichte mit den Massen m1, m2 und m3. Man konstruiere den Schwerpunkt dieser drei Massen.
Aufgabe 47: Tiere in kalten Regionen

Nehmen wir an, wir hätten zwei warmblütige Tiere, die in einer kalten Region leben, links ein kleines Tier, rechts ein grösseres (dargestellt durch die beiden Kugeln in der Abb. links).
Welches Tier passt besser in die kalte Region?
A: Das kleine Tier
B: Das grössere Tier
C: Die Grösse spielt keine Rolle