Aufgabe 1: Boot und Stein
Das Übertreiben bringt die Lösung: Wird der winzige, aber sehr schwere Stein aus dem Boot geworfen, sinkt dieses viel weniger im Wasser ein, das Boot hebt sich und der Wasserspiegel sinkt. Der winzige Stein, der jetzt im Wasser liegt, braucht sehr wenig Platz und bewirkt praktisch keine Änderung des gesunkenen Wasserspiegels mehr.
Übertreiben oder das Betrachten von Extremfällen führt oft auf die richtige Spur zur Lösung.

Quelle: http://en.wikipedia.org/wiki/Traditional_fishing_boat#mediaviewer/File:Coracles_River_Teifi.jpg
Aufgabe 2: Ballspiel auf dem Karussell

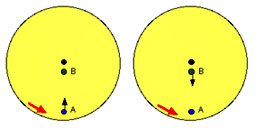
Fig. a) Fig. b)
Fig a): Der Ball, der anfänglich in der Hand von A liegt, erhält vom drehenden Karussell einen starken Geschwindigkeitsanteil nach rechts. Diesen "Schub" behält er bei. Er wird also von A aus gesehen rechts an B vorbeifliegen oder -rollen.
Fig. b): Der Ball in der Hand von B erhält praktisch keinen "Seitenschub" vom Karussell. Er rollt also ziemlich "gerade" von B weg. Während des Rollens bewegt sich aber A ziemlich schnell seitlich weg. Der Ball wird also von B aus gesehen rechts an A vorbei rollen.
Ergebnis: In beiden Fällen wird die werfende Person sehen, dass der Ball nach rechts am Ziel vorbeirollt. (Wie wäre es, wenn das Karussell sich auf die andere Seite drehte?)
Stichwort: Corioliskraft.
Aufgabe 3: Der geheimnisvolle Koffer
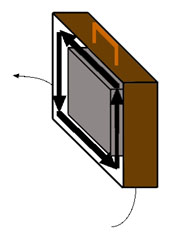
Der Koffer kippt wie in Bild a) gezeigt. Warum? Die Flüssigkeit wird von der Linkskurve "überrascht", will "geradeaus" weiterfliessen und zieht den Koffer deshalb in Richtung der Pfeile wie in Bild a) gezeigt.
Im Technorama Winterthur war einst ein solcher Koffer, der im Innern ein schnell rotierendes Schwungrad verbarg, ausgestellt.
Trug man den Koffer geradeaus, passierte nichts Besonderes, beschrieb man jedoch eine Kurve, begann der Koffer plötzlich zu kippen.
Beim Velofahren lassen wir uns zur Kurveninnenseite kippen. Gleichzeitig werden nun die rotierenden Räder, wie unser Koffer, wieder kurvenauswärts aufgerichtet. Wäre dies nicht der Fall, würden wir umkippen, sobald wir unser Gewicht etwas zur Seite verlagerten. Dies passiert auch, sobald sich die Räder nicht mehr genügend schnell drehen und der "Aufstell-Effekt" damit wegfällt.
Aufgabe 4: Eintauchen
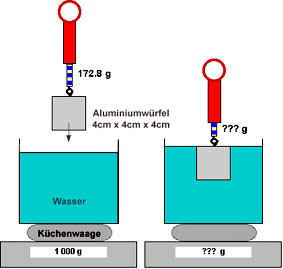
Der Aluwürfel verdrängt 64 Kubikzentimeter Wasser. Dieses wiegt 64 g.
Um so viel wird der eingetauchte Würfel entlastet.
Die Federwaage zeigt also 64 g weniger an, dafür die Küchenwaage so viel mehr.
Aufgabe 5: Elektromagnet
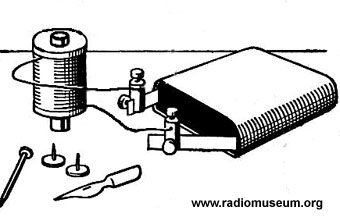
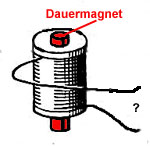
Hätte Herr Schlaumeier recht, so hätten wir eine Wunder-Stromerzeugungsmaschine gefunden! Der ruhende Magnet in der Spule würde uns ständig Strom liefern, ohne dass wir etwas tun müssten.
Elektrische Energie entsteht aber nicht einfach aus dem Nichts. Wir können nur andere Energieformen in elektrische Energie umwandeln, z.B. Körperarbeit (Velodynamo, Sonnenenergie (Solarzelle), Energie eines Flusses, usw.
Wenn Herr Schlaumeier sich bequemt, etwas körperliche Arbeit zu verrichten, wird er mit der Spule und dem Magneten Strom erzeugen können. Wie?
Er muss einfach den Magneten immer wieder aus der Spule herauszhiehen und wieder hineinschieben. So lange er dies tut, entsteht ein Wechselstrom im Draht, allerdings ein sehr kleiner.
Die kleine körperliche Arbeit von Herrn Schlaumeier führt zu einem kleinen elektrischen Wechselstrom.
Dass der Magnet in der Spule bewegt werden muss, damit Strom erzeugt wird, war die Entdeckung von Michael Faraday (1791 - 1867). Das war der Schlüssel für die Entwicklung von Stromgeneratoren.
Natürlich kann auch der Magnet ruhig bleiben und die Spule sich hin und her bewegen.
Zeitgenossen von Faraday, etwa der damalige englische Premierminister, sahen nicht ein, wozu eine Maschine, die elektrischen Strom erzeugte, gut sein sollte...
Aufgabe 6: Elektromotor-Bremse

Ja, das geht. Diese Idee bremst heute auch ultramoderne ICE-Züge. Im Rätsel "Elektromotor" sehen wir, dass ein Elektromotor, der "von aussen", d.h. mechanisch, gedreht wird (hier durch das Gefälle der Strecke) Strom erzeugt.
Heizt dieser Strom den Widerstand auf, wird Energie abgegeben. Diese Energie stammt ursprünglich vom sich drehenden Motor. Der verliert also Energie und wird langsamer.
Auf den ICE-Strecken wird der Strom, den der Motor bei der Talfahrt erzeugt, allerdings nicht zum Heizen einer Drahtspule verwendet, das wäre Energieverschwendung. Vielmehr wird dieser Strom in die Leitung gespeist, die ein bergwärts fahrender ICE benützt. So treibt der talwärts fahrende Zug den bergwärts fahrenden an und wird dabei selber abgebremst.
Nur auf gewissen Strecken im Ausland, wo man den Motorenstrom noch nicht in die Leitung zurückspeisen kann, wird ein Heizwiderstand eingeschaltet. Da verpufft halt die Energie ins Freie, statt einen Gegenzug anzutreiben.
Aufgabe 7: Elektromotor
Herr Schlaumeier hat hier tatsächlich richtig überlegt.
Sobald der Rotor dreht, wird nicht nur Strom benötigt, sondern auch gleichzeitig elektrische Energie erzeugt. Diese fliesst dann zurück ins Netz oder in die Batterie.
Das Elektrizitätswerk schreibt uns auch den so zurückgeleiteten Strom wieder gut.
Sobald eine Last an dern Motor angeschlossen wird, wird er langsamer und gibt damit weniger Energie zurück als er bezieht. Der Eingabestrom wird dann gross und der Motor kann überhitzen. Das passiert z.B. mit einem Stabmixer, der eine so zähe Masse pürieren muss, dass er fast stecken bleibt. Er überhitzt und geht kaputt.
Aufgabe 8: Fadenspule
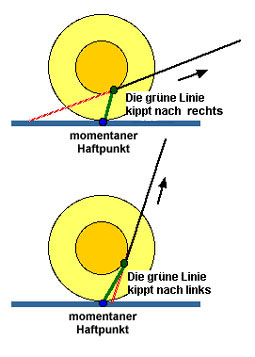
Der Clou an der Sache ist die Haftreibung am blau markierten Auflagepunkt! Für einen kurzen Moment haftet die Spule dort am Boden, bevor sie dann ein Stück weiterrollt und einen neuen Haftpunkt erzeugt.
Wer sich dieses Kippen am blauen Punkt anschaulich vorstellen kann, hat die ganze Sache bereits verstanden.
(Die genaue Berechnung nach den Newtonschen Gesetzen ergibt dann lediglich noch den quantitativen Zusammenhang zwischen den Spulenradien und dem Neigungswinkel des Fadens.)
Je nachdem, wie flach oder steil man zieht, kippt nun die grüne Linie im Bild -und mit ihr die ganze Fadenspule- nach rechts oder nach links.
Irgendwo zwischen "flach ziehen" und "steil ziehen" muss der Wechsel zwischen Rechts- und Linksdrehung der Spule stattfinden. Was passiert dann? - Dann dreht sich die Spule gar nicht, sondern wird lediglich mitgeschleift.
Im Fall R : r = 2 : 1 tritt das reine Mitschleifen bei einem Fadenneigungswinkel von 60° auf. Das lässt sich sogar elementargeometrisch verstehen.
Aufgabe 9: Fallende Körper 1
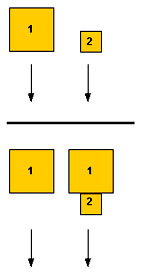
Für den griechischen Gelehrten Aristoteles (384- 322 v. Chr.) war es "klar", dass der jeweils schwerere Körper schneller fallen müsse (das denken auch heute noch viele Personen, die im physikalischen Denken ungeübt sind).
Viele hundert Jahre später zeigte Galileo Galilei (1564 - 1642), dass Aristoteles' Meinung zu einem Widerspruch führt. Er überlegte so:
Wenn Körper 1 tatsächlich schneller fiele als Körper 2, dann machen wir doch einmal ein Wettfliegen zwischen Körper 1 und einer Kombination von Körper 1 und Körper 2 wie im unteren Bild gezeigt: der schwere Körper 1 liegt über dem leichteren Körper 2. Da Körper 2 nach Aristoteles langsamer fällt als Körper 1, bremst er in der Kombination 1 + 2 über ihm liegenden den Körper 1 ab. Die ganze Kombination 1+ 2 fiele dann langsamer als Körper 1 links allein. Aber gleichzeitig würde Aristoteles ja auch behaupten, dass die Kombination 1 + 2 schneller fällt als 1 allein, da sie ja schwerer ist... Ein Widerspruch.
Interessanterweise hätte also Aristoteles durch reines Nachdenken, ohne ein einziges Fallexperiment auszuführen, merken können, dass seine Behauptung falsch war.
Aufgabe 10: Fallende Körper 2
![]()
1. Frage:
Man verbinde in Gedanken die beiden Kugeln mit einem dünnen Stab, so dass eine Hantel entsteht. Wie fällt nun diese Hantel? Sie fällt als Ganzes und zwar so, dass alle ihre Teile stets "miteinander" fallen; kein Teil fällt schneller als der andere. Wären die Kugeln statt mit einem Stab mit einem dünnen Meterfaden verbunden, wäre dieser stets ohne Zugspannung zwischen ihnen ausgestreckt.
Die Kugeln behalten also ihren anfänglichen Meterabstand unverändert bei.
2. Frage, etwas schwieriger:
Die Kugeln behalten ihren Abstand von 1 Meter stets bei. Vom höheren Turm aus haben die Kugeln aber beim Aufschlagen eine höhere Geschwindigkeit als diejenigen, die vom tieferen Turm aus geworfen wurden. Der Wegunterschied von 1 Meter wird also dann schneller zurückgelegt. Der Zeitunterschied zwischen dem Aufprall der beiden Kugeln verringert sich, wenn sie vom höheren Turm aus fallen.
3. Frage:
Der Abstand wird grösser. Warum?
Die vordere Kugel hat stets eine grössere Geschwindigkeit als die hintere Kugel. (Genau genommen ist der Geschwindigkeitsunterschied konstant, aber das braucht man nicht zu wissen.)
Wenn zwei Fahrzeuge so fahren, dass das vordere stets eine höhere Geschwindigkeit hat als das hintere, wird der Abstand zwischen den Fahrzeugen immer grösser.
4. Frage:
Die zweite Kugel imitiert die erste Kugel vollkommen aber stets mit einer zeitlichen Verzögerung von einer halben Sekunde. Sie passiert also jeden Ort, den die erste Kugel durchflogen hat, genau eine halbe Sekunde später ebenfalls. - Dasselbe gilt auch für den Zielpunkt, das Aufschlagen am Boden.
Aufgabe 11: Einwurf beim Fussball

Der Winkel ist nach Berechnungen des Physikers Ken Bray ("Wie man richtig Tore schiesst", Pendo-Verlg) 34°, also flacher als die optimalen 45° bei einer Abwurfmaschine. Das leuchtet gefühlsmässig ein, denn der flachere Winkel ist zwar für die grösstmögliche Weite nicht optimal, dafür kann der Mensch bei diesem flacheren Winkel den Ball kräftiger wegschleudern - und das gibt dem Ganzen dann doch mehr Weite.
Aufgabe 12: heiss und kalt
Versuch 1:
50°
Versuch 2:
Die Antwort ist C. Die Mischtemperatur beträgt nur etwa 10° C. Warum?
Ein Teil der Wärme des Wassers wird benötigt, um das Eis überhaupt zu schmelzen. Das Schmelzen braucht Energie ohne dass dabei die Temperatur steigt.
Wie kann man Wasser und Eis von genau 0° C herstellen? Man gebe viele Eiswürfel mit kaltem Wasser zusammen und warte, bis kein Eis mehr schmilzt. Dann haben Wasser und Eis genau 0°C.
Aufgabe 13: Holzstab balancieren

1B, 1A, 3A, 4B.
Zu Frage 4:
Nein, das geht nun wirklich nicht. Die Reibung zwischen Zeigefinger und Stab muss bei beiden Händen gleich gross sein. Man stelle sich wieder einen Extremfall vor: Der eine Finger sei mit einer klebrigen Flüssigkeit am Stab festgeklebt...
Aufgabe 14: Der berühmte Kletteraffe
![]()

a) b)
Erklärung 1
Durch eine "Film-rückwärts"-Überlegung kommt man der Sache auf die Spur: Nehmen wir an, jemand habe den Vorgang des hinaufkletternden Affen gefilmt. Er zeigt uns jetzt aber diesen Film im Rückwärtsgang. Wir sehen alles rückwärts: Der Affe sinkt. Und was tut das Gewicht? - Das können wir uns gut überlegen: Wir lassen den Affen ohne Wärmereibung sinken, indem wir uns vorstellen, dass das Tier das Seil kurz loslässt, um es gleich darauf wieder zu halten. Dabei fällt der Affe ein Stück nach unten und hängt dann wieder fest.
Was macht das Gewicht dabei? Sobald der Affe losgelassen hat, wird auch das Gewicht fallen, und zwar gleich schnell und weit wie der Affe. Am Schluss dieses kleinen Falles sind Affe und Gewicht wieder im Gleichgewicht, aber beide liegen jetzt ein Stück tiefer, jedoch immer noch auf der gleichen Höhe.
Das war "Film rückwärts". - "Film vorwärts" ist jetzt die Umkehrung davon: Steigt der Affe, steigt auch das Gewicht. Affe und Gewicht sind immer gleich hoch. Am Schluss sind Affe und Gewicht ganz oben bei der Rolle.
Erklärung 2
Eine völlig gleichartige Situation ist folgende: Zwei gleich schwere Personen stehen je auf Rollschuhen. Sie stehen sich ein einem gewissen Abstand gegenüber und halten ein gespanntes Seil oder eine dünne Stange zwischen sich.
Person A beginnt nun am Seil oder an der Stange vorwärts zu hangeln, während Person B passiv das andere Ende hält. - Was passiert? - Diese Situation kann man sich leichter vorstellen, obwohl sie gleichwertig ist zur Situation mit dem Affen, der Rolle und dem Gegengewicht. (Wer noch etwas Schwerkraft einbauen will, kann sich beide Rollwege zur Mitte hin etwas ansteigend denken.)
Erklärung 3
Eine weitere Möglichkeit, der Sache auf die Spur zu kommen, ist folgende (s. rechtes Bild b):
Wir denken uns Affe und Gegengewicht zu einem einzigen, doppelt so schweren Affen verbunden, der sich selber in die Höhe zieht. Er ist am rechten Seil befestigt und zieht sich am linken Seil hoch. Der ganze "Doppelaffe" steigt in die Höhe.
Aufgabe 15: Krafttraining

Wo findet aber die Arbeit statt, die uns bei solchen Übungen erschöpft? In unseren Muskeln. Die beginnen unheimlich schnell zu "zucken".
Wenn wir erschöpft werden, wird dieses Zucken unregelmässiger, dann beginnen wir auch äusserlich zu zittern. Diese inneren Muskelbewegungen sind die Arbeit, die wir bei solchen Kraftübungen errichten.
Aufgabe 16
Abb. 1: Antwort A.
Abb. 2: Antwort B.
Abb. 3: Antwort B.
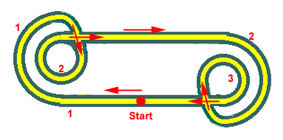
In Abb. 1 wird am Faden gezogen und der Zug wirkt nicht exakt rechtwinklig zur Bahn:
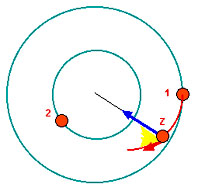
Der gelbe Winkel ist kein rechter Winkel. Der Zug (blauer Pfeil zur Mitte) wirkt deshalb ein klein wenig auch in Fahrtrichtung der Kugel und beschleunigt sie. Die Geschwindigkeit wird erhöht.
Eine andere Erklärung ist folgende: Durch das Ziehen an der Schnur mussten wir Arbeit verrichten: Wir haben Energie in die Vorrichtung gesteckt. Die einzige Art, wie sich diese investierte Energie "ausleben" kann, besteht darin, die Geschwindigkeit der Kugel zu erhöhen.
In Abb. 2 hingegen (Aufwickeln des Fadens am Sechseckpfosten) wirkt der Fadenzug immer exakt rechtwinklig zur Bahn. Die Bahnabschnitte sind exakte Kreisbogenstücke; man kann sie mit dem Zirkel nachkonstruieren. Eine Beschleunigung findet deshalb nicht statt. Die Geschwindigkeit bleibt gleich. (Es hat auch niemand zusätzliche Energie ins System einfliessen lassen.)
Da die Bahnen aber immer enger werden, verkürzen sich bei konstanter Geschwindigkeit die Zeiten für eine Umdrehung zunehmend. Das sieht auf den ersten Blick nach "schneller werden" aus, ist es aber nicht.
Abb. 3: Die Geschwindigkeit muss konstant bleiben. Warum? Die Schienenkräfte wirken erneut genau rechtwinklig zur Fahrtrichtung und können somit das Fahrzeug nicht beschleunigen.
Würde die Geschwindigkeit tatsächlich höher werden, könnten wir eine fantastische Maschine konstruieren (s. Bild links):
Der Wagen fährt mit Geschwindigkeit 1 in den äusseren linken Kreis ein. Dann befährt er den inneren Kreis. Würde er jetzt schneller (Geschwindigkeit 2), so würde er den rechten äusseren Kreis mit dieser erhöhten Geschwindigkeit befahren und beim Einfahren in den rechten, kleinen Kreis erneut beschleunigt werden (Geschwindigkeit 3). Mit dieser Geschwindigkeit würde er wieder zum Startpunkt kommen und eine neue Runde mit noch höherer Geschwindigkeit beginnen.
Der Wagen würde so von selber, ohne Energiezufuhr, immer schneller werden.
Ein solches Perpetuum mobile ist jedoch unmöglich - also muss die Geschwindigkeit konstant bleiben.
Aufgabe 17: Kräfte
Die Antwort ist D. Tatsächlich ist diese Kraft grösser als die Gewichtskraft der Kugel. Warum?
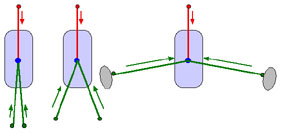
a) b) c)
Ein Wagen werde von einer Person mittels der roten Stange vorwärts gestossen. An den beiden grünen Stangen stossen zwei Personen dagegen und versuchen, den Wagen zu stoppen. Die grünen Stangen können in verschiedene Richtungen gedreht und dann stabil fixiert werden.
Bild a) Hier kann der Wagen leicht gestoppt werden. Die beiden Personen an den grünen Stangen brauchen je etwa die Hälfte der roten Kraft.
Bild b) Die grünen Stangen sind weiter nach aussen gedreht. Jetzt wirkt die Stosskraft der Personen an den grünen Stangen nicht mehr voll in Gegenrichtung zur roten Kraft. Ein Teil der Kraft wirkt seitlich. Die grünen Personen brauchen mehr Kraft, um den Wagen zu stoppen.
Bild c) Eine Extremposition. Hier geht fast die gesamte Stosskraft längs der grünen Stangen zur Seite. Die beiden Personen an den grünen Stangen stossen zum grössten Teil gegeneinander. Nur ein geringer Teil ihrer Stosskraft wirkt der roten Kraft entgegen, der grösste Teil wird in einen "Zweikampf" der beiden grünen Personen gegeneinander investiert. Diese müssen viel mehr Kraft aufwenden, um den Wagen zu stoppen als die rote Person.
Der Wagen könnte auf seiner Fahrt sogar die grau gezeichneten Blumentröge wegstossen, falls diese nicht genügend Gegenkraft aufbringen. Der Wagen ist längs der grünen Stangen fast nicht zu stoppen. Er übt auf die beiden grauen Hindernisse eine riesige Kraft aus. Genau genommen sind es die Hindernisse selber, die aufeinander diese grosse Kraft ausüben. Bei der Kugel im Spalt ist es genau so:
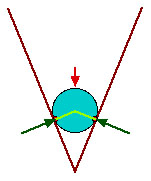
So seitlich schräg muss dem Kugelgewicht viel mehr Kraft entgegengesetzt werden, mehr sogar als das Kugelgewicht selber. Der grösste Teil der Kraft rührt daher, dass die beiden Spaltwände via Kugel selber gegeneinander drücken. Bei einem Spalt von 45° wirkt bei jedem Auflagepunkt etwa das 1.3-fache Gewicht der Kugel.
Aufgabe 18: Möwenfüsse
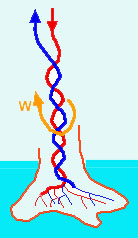
Die Antwort ist C.
Die Wärme* in den rot gezeichneten Blutbahnen "wendet" schon vor den Füssen, indem das kalte, zurücklaufende Blut (blau) aufgewärmt wird. Dadurch kommt kein sehr kaltes Blut in den Körper zurück. Umgekehrt wird das Blut, das in Richtung Füsse fliesst (rot) abgekühlt und die Wärme gelangt nicht via Füsse in den kalten Boden.
Es ist dies ein Wärmeaustauscher.
Link:
http://www.spektrum.de/frage/wieso-erfrieren-voegeln-im-winter-nicht-die-fuesse/905710
*) Diese Formulierung ist physikalisch nicht korrekt, denn "Wärme" ist kein Stoff, der "wenden" kann. "Wärme" ist ein Vorgang, nämlich Energieübertragung aufgrund eines Temperaturunterschiedes. Das Nomen "Wärme" steht also nicht für einen Stoff, sondern für einen Energieübertragungs-Vorgang.
Korrekter müssten wir also punkto Möwenbeine sagen: Der Wärmeenergieaustausch findet bereits im Bein statt und nicht zwischen Füssen und kaltem Boden.
Aufgabe 19: Fallende und rollende Zylinder
Frage 1: Klar, beide kommen gleichzeitig unten an, denn alle Körper fallen - ohne Luftwiderstand - gleich schnell, ob schwer oder leicht.
Frage 2: Antwort b; der Holzzylinder ist schneller. Beim metallenen Hohlzylinder ist die gesamte Masse weit aussen angebracht und wird so im Durchschnitt auf einem weiteren Weg (weiter aussen) herumgedreht als beim Holzzylinder. Das braucht mehr Energie und folglich kommt der hohle Metallzylinder langsamer ins Rollen.
Man kann folgenden Versuch ausführen: Man setze sich auf einen Drehstuhl, in jeder Hand einen schweren Gegenstand (z.B. eine Hantel) haltend. Versetzt man sich nun in Drehung kann man die Geschwindigkeit regulieren: Streckt man die Arme aus, verlangsamt sich das Tempo, zieht man die Arme an, dreht man sich schneller.
Aufgabe 20: Zwei gleitende Körper
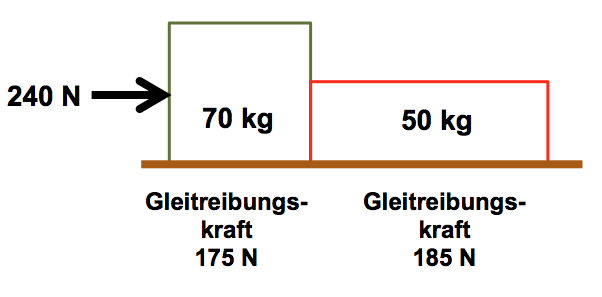
Wir betrachten Block 1 und 2 als Ganzes: 120 kg.
Kräftesumme auf dieses Gesamtgebilde: 240 N – 175 N – 185 N = -120 N.
Die Beschleunigung ist folglich a = F / m = -1 m / s2.
Man beachte: Die Beschleunigung ist negativ, obwohl sich das
Gebilde nach rechts bewegt; das bedeutet, dass die Bewegung
abgebremst wird mit a = -1 m / s2.
Aus a = - 1 m /s2 ergeben sich die auf die Teilkörper wirkenden
Kräfte:
Auf Körper 1 wirken - 70 N, auf Körper 2 wirken - 50 N.
Dies ergibt dann die richtige Beschleunigung a = - 1 m / s2.
Sei X die gesuchte Kraft von Körper 1 auf Körper 2.
Für Körper 2 gilt: X - 185 N = - 50 N. Es folgt: X = 135 N.
Probe mit Körper 1:
Für Körper 1 gilt: 240 N -175 N - X = - 70 N. => X = 135 N.
Geogebra-Simulation mit variabler Kraft von links: hier.
Aufgabe 21: Schwimmen
Damit das Wasser den eingetauchten Würfel gerade schwebend in Ruhe lässt, muss er punkto Gewicht und Volumen dem Wasser völlig gleichen. Dann "erkennt" ihn das Wasser nicht als etwas "Fremdes". Der untergetauchte Literwürfel muss also das Gewicht einer 1-kg-Masse aufweisen. Das ist der Fall, wenn ich den 800-Gramm-Klotz oben noch mit einem 200-Gramm-Marktgewicht beschwere.
Aufgabe 22: Waage
B. Es handelt sich hier nicht um eine gewöhnliche Balkenwaage. Dort führt ein Verschieben des Gewichts zu einem Ungleichgewicht. Bei dieser Rhomboid-Waage spielt es keine Rolle, wie weit aussen das Gewicht hängt.
Aufgabe 23: Wandspiegel
C. Siehe Skizze: gelber Bereich. Die Strecke AB (s. Bild) ist halb so lang wie die Körpergrösse der Person. Es genügt, wenn der Spiegel diese Grösse aufweist.

Aufgabe 24: Wasser fliesst aus
C trifft zu.
Beim Gefäss rechts füllt das austretende Wasser (fast) den ganzen Rohrquerschnitt aus (ca. 90%).
Beim mittleren Gefäss füllt der Strahl nur ca. 62% des Querschnitts aus. Das Wasser kann an der scharfen Kante nicht "sofort umbiegen". Der Strahl ist enger als die Ausgussöffnung.
Beim Gefäss links ist es noch extremer. Der Strahl füllt nur ca. 50% des Querschnitts aus.
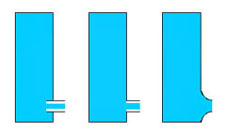
Aufgabe 25: Wasserdruck 1
Die richtige Antwort ist A.
Der Bodendruck hängt nur von der Wasserhöhe ab.
Bei b wird ein Teil des Wassergewichts von den schrägen Seitenwänden aufgefangen.
Wie sieht es bei e aus? Hier wirk ja wenig Wasser. Es entsteht unten trotzdem eine Kraft, die grösser ist als das Gewicht des beteiligten Wassers. Wie ist das möglich? Die zusätzliche Kraft entsteht durch die Decke der unteren breiteren Kammer. Zum Vergleich: Auch wir können auf einer Personenwaage mehr Gewicht anzeigen lassen, als wir tatsächlich haben, wenn wir uns in einem niedrigen Raum beim Wägen noch gleichzeitig oben an der Decke abstossen. Ähnliches geschieht bei den Gefässen c und e.

Aufgabe 26: Druck in einem Wasserkübel
Die richtige Antwort ist B. Der Druck bei B ist grösser. Nicht nur der Taucher spürt den grösseren Druck, sondern auch die Gefässwand. Die Belastung der Gefässwand nimmt von oben nach unten zu. Deshalb sind Staudämme unten auch breiter als oben.
Anschlussrätsel:
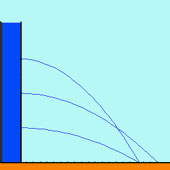
Die überraschende Lösung ist hier C: Beide Strahlen kommen gleich weit, wenn die Löcher symmetrisch zur Zylindermitte liegen, weil der Zylinder direkt auf dem Boden steht. Das Wasser beim unteren Loch schiesst zwar mit mehr Druck und somit schneller heraus, es landet aber nach sehr kurzer Zeit bereits auf dem Boden. Tipp: ausprobieren. Man trifft gelegentlich Bücher an, in denen dieser Versuch krass falsch gezeichnet ist.
Wo müsste das Loch angebracht werden, damit das Wasser möglichst weit spritzt? Genau in der Zylindermitte.
Das Bild zeigt die Situation, wenn der Zylinder direkt auf dem Boden steht:
Aufgabe 27: Wasserschlacht am Brunnen
Fall A: Die überraschende Antwort ist C. Der Druck auf gleicher Höhe über Boden ist bei beiden Öffnungen derselbe. Jedes Wasserteilchen in der Nähe der Öffnung (Düse oder nicht) erfährt die gleiche Kraft.
Fall B: Brunnen weit weg vom Reservoir:
Die Antwort ist B: Es ist die Reibung in den langen Zuleitungen, die bewirkt, dass eine Düse überhaupt etwas nützt.
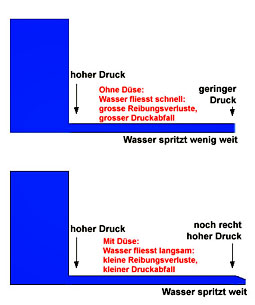
Das Wasser, das durch die langen Zuleitungen fliesst, erzeugt Reibung und diese verwandelt Energie in Wärme. Wenn wir also das Wasser aus dem Reservoir durch lange Schläuche schicken, spritzt es durch diesen Energieverlust nicht mehr so stark heraus wie vorher direkt am Reservoir.
Die Reibung ist stark, wenn das Wasser schnell durch die Leitung fliesst und schwach, wenn es langsam fliesst. Montiere ich nun eine Düse, die in der gleichen Zeit nur noch halb so viel Wasser durchlässt wie vorher, fliesst das Wasser nur noch halb so schnell: Die Reibungsverluste werden jetzt kleiner. Der anfängliche Druck aus dem Reservoir wird nun besser verwertet. In den Leitungen baut sich ein grösserer Druck auf, der das Wasser am Schlauch-Ende beim Übergang zum normalen Luftdruck weiter spritzen lässt als vorher.
Stelle ich die Düse breiter ein, fliesst das Wasser schneller, die Reibungsverluste werden grösser, der Druck in der Leitung nimmt ab, das Wasser spritzt weniger druckvoll heraus.
Die Reibungsverluste kann man fast ganz zum Verschwinden bringen, wenn man die Brunnenröhre bis auf ein ganz winziges Löchlein zuhält. Das Wasser spritzt dann fast so druckvoll heraus, wie wenn das Loch direkt am Reservoir angebracht wäre.
Die langen Leitungen und die Reibung sind also Schuld, dass eine Düse etwas bewirkt.
Rostende Leitungen: Wenn bei einem Wasserhahn der Druck allmählich nachlässt, kann dies ein Zeichen für Rost in den Leitungen sein. Rost erhöht die Reibungsverluste und führt zu einem Druckabfall.
Quellen: L.C.Epstein, Epsteins Physikstunden, Birkhäuser, 1989 und Hans J.Paus: Physik, Hanser-Verlag, 1995.
Aufgabe 28: Wettrennen
Die Antwort ist C: Carla wird immer noch gewinnen.
Wenn Carla 100m gelaufen ist, befindet sie sich bei der 95m-Marke, da sie ja 5m vor der Startlinie losgerannt ist. Adrian ist in dieser Zeit 95m gelaufen. Sie erreichen also die 95m-Marke gleichzeitig. Weil Carla etwas schneller rennt, wird sie die verbleibenden 5m schneller als Adrian durchlaufen und immer noch gewinnen. Anders wäre es, wenn Carla auf der Startlinie loszöge und Adrian 5m Vorsprung erhielte. Dann erreichten sie das Ziel gleichzeitig.
Aufgabe 29: Wärme
Frage 1: Die Wärme der Sonne erreicht uns auch über das Vakuum des Weltalls in Form von Wärmestrahlung (Infrarotstrahlung). Diese pflanzt sich wie Lichtwellen auch im Vakuum fort. Wäre Wärme nur an Materie gebunden, gäbe es im Weltall keine Temperatur. Im Vakuum des Weltalls herrscht aber eine Temperatur von ca. minus 270 Grad Celsius, verursacht durch Wärmestrahlung. Das sind etwa 3° über dem absoluten Nullpunkt.
Frage 2: Antwort B. Ein dunkler Körper nimmt die Wärmestrahlung in grösserem Mass auf; der helle reflektiert einen grossen Teil der Strahlung gleich wieder.
Frage 3: Antwort C: Hier spielt die Wärmestrahlung keine Rolle. Die Wärme wird über direkten Kontakt weitergeleitet.
Frage 4: Antwort B. Helle Körper reflektieren einen grossen Teil der Wärmestrahlung. Von selber strahlen sie aber weniger Wärme ab als dunkle Körper.
Deshalb bietet ein heller Hausanstrich Vorteile: Im Sommer wird ein grosser Teil der Wärmestrahlung reflektiert; bei Kälte wird weniger Wärmestrahlung abgegeben.
Sind Häuser dicht nebeneinander gebaut, ist helle Farbe ebenfalls von Vorteil, da sie das Licht reflektiert und nicht verschluckt. So erhalten die Nachbarhäuser indirektes Licht.
Helle Farbe wird, da die Strahlung weniger absorbiert wird, auch weniger schnell zerstört.
Quelle: Lewis C.Epstein: Epsteins Physikstunde, Birkhäuser 1989.
Frage 5: Antwort B. Wird Eis von 0°C erhitzt, schmilzt es und es entsteht Wasser von 0°C. Eine Temperaturerhöhung hat also nicht stattgefunden. Die Wärme wurde nicht zur Erhöhung der Temperatur gebraucht, sondern zum Schmelzen des Eises. Wird Wasser von 100°C erhitzt, entsteht Dampf von 100°C: erneut keine Temperaturerhöhung.
Aufgabe 30: Zerreissprobe
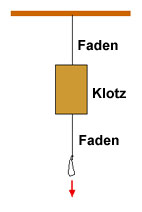
Die Antwort ist C. Zieht man langsam an der Schlaufe nach unten, wird der Faden oberhalb des Klotzes reissen, da am oberen Faden zusätzlich zum Zug das Gewicht des Klotzes wirkt.
Zieht man aber sehr schnell, mit einem Ruck, wird der Faden unterhalb des Klotzes reissen, weil der Klotz wegen seiner trägen Masse den Ruck nicht nach oben weitergibt.
Aufgabe 31: Breite Spritze, schmale Spritze
Frage 1: Antwort A.
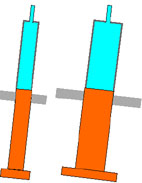
Richten wir in Gedanken die Spritzen nach oben und spritzen das Wasser in einen oben aufgehängten Kübel hinein. Dieses Hinaufpumpen benötigt Energie. Die stammt von der Kraft, mit der wir den Kolben langsam hineindrücken. Energie = Kraft mal Weg. Die hineingesteckte Energie ist also bei beiden Kolben gleich gross (gleiche Kraft, gleicher Weg). Bei der breiten Spritze wird aber total mehr Wasser nach oben befördert, das kann bei gleicher Energie-Investition nur bedeuten, dass das Wasser weniger hoch hinaufgepumpt werden konnte als bei der schmalen Spritze. Es ist wie beim Hochwerfen eines leichten und eines schweren Balles: Bei gleichem Energieaufwand werfe ich den leichteren Ball höher hinauf.
Frage 2:
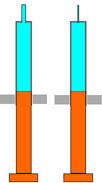
Antwort C. Wieder ist unsere Energieinvestition in beiden Fällen gleich gross. Zudem ist hier die hochgepumpte Wassermenge ebenfalls gleich gross. Die Pumphöhe ist somit in beiden Fällen dieselbe.
Man beachte: Die Zeit spielt hier keine Rolle. Bei der Spritze mit der schmalen Düse dauert der Vorgang einfach länger (d.h. die Leistung ist kleiner).
Aufgabe 32: Warum gibt es Koloratursopranistinnen, aber keine Koloraturbässe?

Nehmen wir an, ein Bass habe einen Ton von f=100 Hz (ca. ein G) als Staccato, das ΔT=0.2s lang sei, zu singen. Dann erreichen seine und unsere Ohren 100⋅0.2 = 20 Schwingungen. Singt er einen Ton von beinahe 105 Hz, so erreichen unsere Ohren ebenfalls nur 20 Schwingungen. Der Sänger und wir können also in dieser gesungenen Kürze von 0.2s einen 100-Hz- und z.B. einen 104-Hz-Ton nicht unterscheiden. Ein 104-Hz-Ton ist jedoch gegenüber einem 100-Hz-Ton bereits um mehr als einen Viertelston zu hoch, das heisst er tendiert bereits gegen das GIS, ohne dass wir dies bemerken können.
Die Klangerkennung funktioniert somit bei derart kurzen Tonkoloraturen in dieser Tiefe nicht mehr. Der Sänger kann seine Töne nicht mehr klar erkennen (und gegebenenfalls nachkorrigieren) und auch die Zuhörenden vermissen eine klare Tonzuordnung.
Ein schneller Triller G-GIS in dieser Tiefe würde von uns als Tonbrei wahrgenommen.
Experiment mit Klavier:
Man spiele mit zwei benachbarten tiefen Tönen (z.B. 65 Hz, C und 69 Hz, CIS) einen zuerst langsamen und dann immer schneller werdenden Triller. Ab wie vielen Tönen pro Sekunde verschwimmt der Triller zu einem Klangbrei, in welchem C und CIS nicht mehr auseinanderzuhalten sind?
Zusammengefasst: Je höher der Ton, desto kürzer darf er erklingen, um in der Tonleiter sicher lokalisiert werden zu können. Je tiefer der Ton, desto länger muss er erklingen, um im Tonleitersystem erkennbar zu sein.
Kürzere Zeitspanne des Erklingens bedingt schlechtere Lokalisierbarkeit im Tonleitersystem, längere Zeitspanne hat bessere Lokalisierbarkeit zur Folge. Dieser Antagonismus verschärft sich bei tiefen Tönen.
Etwas genauere Erläuterung:
Sei
f die Frequenz des Tones, der ΔT Sekunden lang ertöne. Sei n die Anzahl Schwingungen, die unser Ohr treffen. Es gilt n=f⋅ΔT.
Erhöhen wir nun f um Δf, sodass gilt: (f+Δf)⋅ΔT=n+1. Es folgt: f⋅ΔT+Δf⋅ΔT=n+1 und deshalb n+Δf⋅ΔT=n+1 oder Δf⋅ΔT=1.
Es ist also Δf=1/ΔT.
Wird ein Ton, der ΔT Sekunden lang ertönt um weniger als Δf erhöht, so treffen immer noch gleich viele Schwingungen unsere Ohren und wir können nicht sagen, ob die Frequenz nun genau f oder etwas zwischen f und f+Δf beträgt.
Beträgt ΔT eine Fünftelsekunde, so ist also
Δf=5Hz und zwar unabhängig von der Frequenz f des Tones.
Bei tiefen Tönen können 5Hz gut und gerne mehr als einen Viertelton ausmachen, bei hohen Tönen machen 5Hz nicht viel aus; 885Hz ist z.B. nur etwa um einen Zwanzigstelton höher als 880Hz, was kaum hörbar ist.
Das heisst: Die relative Unsicherheit Δf/f ist bei tiefen Tönen gross (bei ΔT=0.2s und f=100Hz 5%), bei hohen klein (bei ΔT=0.2s und f=880 Hz ca. 0.57%). Eine Sopranistin kann somit gut Tonfolgen in der Kürze von 0.2 Sekunden singen und sofort sicher lokalisieren, ein Bass nicht.
Das Beispiel findet sich in Gerthsen: Physik, D. Meschede, 22. Auflage, Springer-Verlag, Heidelberg, 2004, einer Fundgrube an überraschenden Aufgaben.
Bildergalerie


Links: Rechteckimpuls der Länge ΔT=1s.
Rechts: Das zugehörige Frequenzspektrum. Wesentliche Breite: Δf=1/ΔT=1Hz
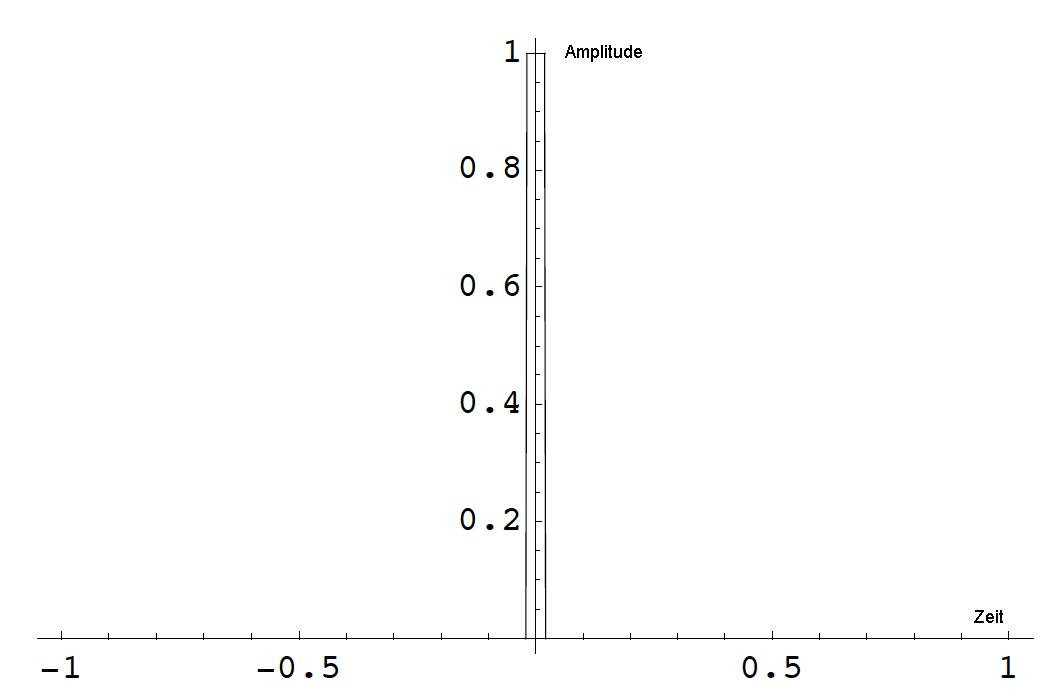

Links: Rechteckimpuls der Länge ΔT=0.04s.
Rechts: Das zugehörige Frequenzspektrum. Wesentliche Breite: Δf=1/ΔT=25Hz.
Man sieht erneut: Je kürzer der Impuls, desto breiter das wesentliche Frequenzspektrum.

oben: reine Kosinusschwingung 10Hz während 1s. Man erkennt die Hörunsicherheit beim Ein- und Ausschwingen der zeitlich begrenzten Schwingung.
Weitere Fourierspektren:
waagrechte Achse: Kreisfrequenz ω=2πf
senkrechte Achse: Amplitude


Links: Spektrum einer reinen Kosinusschwingung 110Hz, 1 s; rechts: dito nur noch 0.33s
Frequenzspannweite links ca. 2Hz, rechts ca. 6Hz, das ist in dieser Tiefe fast ein Halbtoncluster.

Oben: Spektrum einer reinen Kosinusschwingung 600Hz, Dauer 1s.
Frequenzspannweite erneut ca. 2 Hz.
Dauert der Ton 0.33s, so ergibt sich wiederum eine Frequenzspannweite von 6Hz, was in dieser Tonhöhe weniger als einen Zehntelston ausmacht: Der Ton wirkt auch in dieser Kürze immer noch sehr rein.
Spektrum eines Rechteckimpulses mit Geogebra

Ursprüngliche Funktion: Rechteckimpuls mit Amplitude 1 und Länge 2τ, symmetrisch zur y-Achse. Periode T, d.h. der Impuls wiederholt sich nach jeweils T Sekunden (im Bild links nicht gezeichnet).
Geogebra-Modell:
Was passiert im Frequenzspektrum, wenn man T sukzessive erhöht? Die Spektrallinien wachsen immer enger zusammen. Wird T unendlich (das bedeutet, dass der nächste Impuls überhaupt nicht mehr erscheint, d.h. dass wir, wie im Bild gezeigt, einen Einzelimpuls haben), entsteht ein kontinuierliches Spektrum.
Im Geogebra-Modell haben wir die Skalierung der Amplituden-Säulen so gewählt, dass die Säulenfläche und nicht die Säulenhöhe die Amplitude B(n) angibt.
Erneut sieht man: grosses Tau bedeutet schmales Frequenzspektrum, kleines Tau bedeutet
breites Spektrum.
Aufgabe 33: Rollendes Trottoir
Die richtige Antwort ist B: Max trifft zuerst wieder bei A ein. Schnellerer Hinweg und langsamerer Rückweg bei Linda kompensieren sich nicht.
Sei die Länge der Strecke AB gleich s.
TLinda= s/(v+w)+s/(v-w) = 2sv/(v2-w2)
TMax= 2s/v = 2sv/v2 < TLinda, falls 0 < w < v.
Beispiel: v = 2w. Dann beträgt Lindas Zeit das 4/3-fache von Max' Zeit.
Aufgabe 34: Tacho-Abstandsregel

Die Antwort ist nicht eindeutig festzulegen. Falls man genau so stark bremsen kann wie das vordere Fahrzeug, ist die Regel vernünftig, denn dann muss nur die Reaktionszeit tR einberechnet werden, für die gilt: tR=s/v.
Da die Aufmerksamkeit auf Autobahnen in der Regel etwas nachlässt, ist die Zweisekundenregel eher knapp; eine Drei- bis Viersekundenregel wäre angemessener.
Bei 50km/h ergibt sich eine Reaktionszeit von 1.8s, was bei erhöhter Aufmerksamkeit innerorts ebenfalls genügen sollte. Dies entspricht ebenfalls der Zweisekundenregel.
Aufgabe 35: Gleitendes Boot ("Stiefeln")
Antwort A: ja; man nennt dies "stiefeln".
Dann müsste aber das Boot etwas schneller vorankommen als das Flusswasser. Trifft dies zu? - Ja.
Wie erklärt sich dies?
Das Flusswasser strömt nicht überall gleich schnell (am schnellsten an der Oberfläche und in der Flussmitte). Dadurch entstehen infolge interner Wirbel und Gleitverschiebungen Energieverluste, die sich auf die Strömungsgeschwindigkeit des Wassers auswirken und diese herabsetzen.
Das feste Boot ist frei von solchen inneren Wirbeln und kann so strömen, wie Wasser, das keinen inneren Verlusten ausgesetzt ist. Es strömt etwas schneller als Wasser.
Links dazu:
Lexikon der verblüffenden Erkenntnisse
Gerthsen: Physik
"Stiefeln"
Man vergleiche hierzu eine sich langsam und träge vorwärts bewegende Menschenmasse, die eine Person im Triumph über sich trägt (Crowdsurfing) und schneller vorwärts befördert als sich die Masse selber weiterbewegt, da sich einige Teile der "Fliessmasse", nämlich die Arme, zwischenzeitlich stärker nach vorn bewegen als die Durchschnittsdrift der Masse.

Aufgabe 37: Optimal bemessener Balken bezüglich Tragkraft
d2b = maximal und zudem muss gelten (Pythagoras): d2+b2=1.Es folgt: d2=1-b2 und folglich d2b=(1-b2)b=b-b3=maximal=:f(b).
Ableitung: f '(b)=1-3b2=0 => b=1/√3. d=√2/√3.
Es folgt: d : b = √2 : 1.
(Das ist dasselbe Verhältnis, das auch ein DIN-A4-Rechteck hat.)

Aufgabe 38a: Was vertauscht ein Spiegel eigentlich?
Ich nehme einen Pfeil ("Vektor") in die Hand und bemerke: Es werden stets nur die Vektorkomponenten senkrecht zur Spiegelfläche vertauscht. Absolut gesehen vertauscht der Spiegel diese Komponenten und nichts anderes.
Aufgabe 38b:
Ausprobieren!
Aufgabe 39: Drehteller


r(t) für ω=1s-1, d.h. Umlaufzeit des Tellers=6.28s, R=1m, r0=0.01m.
Gesamtzeit bis zum Erreichen der Peripherie ca. 4.6s.
Aufgabe 40: Drehteller 2: Film rückwärts (Zeitumkehr)
Die Antwort ist B: Die Beschleunigung wird mit der Zeitumkehr nicht umgekehrt.
Man stelle sich den "Film-rückwärts-Ablauf" vor: Der Wagen bewegt sich von der Peripherie her zunächst schnell nach innen und wird immer langsamer. Die Geschwindigkeit (erste Ableitung des Ortes) hat sich umgedreht. Die Beschleunigung (zweite Ableitung des Ortes) wirkt jedoch immer noch nach aussen und bremst den Wagen so langsam ab.
Zusatzfrage:
Antwort A: Die Änderung der Beschleunigung ist im "Film-rückwärts-Ablauf" zuerst stark. Dann, nach innen, wird sie zunehmend schwächer. Die Beschleunigungsänderung (dritte Ableitung des Ortes) ändert sich von ursprünglich "schwach-stark" zu "stark-schwach".
Zeitumkehr formal im Beispiel von Aufgabe 39:
t wird durch -t ersetzt. Die Ortsfunktion wird in der Zeitumkehr r(t)=R⋅e-ωt.
Aufgabe 41: Crash
Richtige Antwort: B, ca. 23 km/h.
Sei s = Knautschdistanz, t = Aufprallzeit bis Stillstand, v = Anfangsgeschwindigkeit, a = negative Beschleunigung beim Aufprall.
Es ist s = a⋅t2/2, d.h. t2=2s/a. Ferner ist v = a⋅t , d.h. v2=a2⋅t2. Es folgt:
v2=2as und v=√(2as).
Mit a = 40 m/s2 und s = 0.5 m ergibt sich v = 6.32... m/s = 22.77 km/h:
Ziemlich erstaunlich! Ist man angegurtet und öffnet sich der Airbag nicht, müssen die Gurte also bereits bei bescheidenen 23km/h ca. 4g aushalten.
Aufgabe 42: Traktorräder
Die für ein starkes Zugfahrzeug notwendige starke Untersetzung liefert bei kleiner Drehzahl ein hohes Drehmoment T auf die Antriebsachse.
Ein allzu grosses Drehmoment T führt jedoch zur Überschreitung der maximal möglichen Haftreibungskraft μ⋅G (G=Gewicht auf die Hinterräder; μ=Haftreibungskoeffizient) und zum Durchdrehen der Räder.
Für das maximal mögliche Drehmoment T gilt
T=
μ⋅G⋅r oder T/r=μ⋅G (r=Radius Hinterrad).
Damit der Wert μ⋅G nicht überschritten wird (ansonsten Durchdrehen der Räder), muss bei grossem T also auch r relativ gross sein: grosse Hinterräder.

Weiterer Vorteil grosser Hinterräder:
grössere Auflagefläche
Nachteil:
In die Drehung grosser Räder muss mehr Energie investiert werden.
Aufgabe 43: Beschleunigungsrekord

B: nein. Erhöht man M, erhöht sich zwar die Haftreibung, aber gleichzeitig wird das Fahrzeug auch träger und erzielt eine langsamere Beschleunigung a.
Es ist
μ⋅M⋅g = M⋅a oder a = μ⋅g.
Bei der vorliegenden Weltrekordfahrt wurden 100km/h = 27.8m/s in 1.513s erreicht. Es ist a= 27.8/1.513 m/s2 = 18.4 m/s2.
Das ergibt ein μ von a/g = 1.8.
Das ist viel höher als die entsprechenden Koeffizienten auf normalen Strassen (0.4 bis 0.9). Die Verbindung Reifen / Strasse musste also speziell "haftfest" sein. Zudem war jedes Rad individuell angesteuert.
Im normalen Strassenverkehr beginnt zum Glück bei zu forschem Beschleunigen das ABS zu wirken.
Aufgabe 44: Velospuren im Schnee
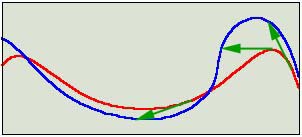
a) Das Hinterrad nimmt stets den kürzeren Weg als das Vorderrad. Deshalb: Rot = Hinterradspur, Blau = Vorderradspur.
b) Wir denken uns ein etwas vereinfachtes Fahrzeug (Bild unten). Es besteht nur aus einem Hinterrad (gelb) mit zwei Griffen dran, an denen wir es führen können. Der Velorahmen wird durch einen Pfeil (grün) ersetzt, der nach vorne zeigt.
Wir führen das Hinterrad an den Griffen der roten Hinterradspur nach. Die Spitze S des grünen Pfeils bewegt sich dann auf der Vorderradspur.
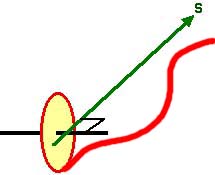
Wir bemerken, dass der grüne Pfeil in jeder Situation tangential von der roten Kurve "wegschaut". Die Vektorlänge zwischen Hinterrad- und Vorderradspur muss stets gleich bleiben. Dies ist nur dann der Fall, wenn wir das Velo von rechts nach links führen.
Aufgabe 45: Senkrechte Kreisbewegung
a) Antwort C ist richtig.
Man kann (siehe Teilaufgabe c) so schwingen, dass am höchsten Punkt die Fadenkraft ganz verschwindet und die Zentripetalkraft allein von der Gewichtskraft m⋅g aufgebracht wird. Unten muss die Fadenkraft die notwendige Zentripetalkraft liefern und erst noch das Gewicht m⋅g kompensieren.
b) Antwort C ist richtig.
Am höchsten Punkt hat die Masse eine gewisse kinetische und eine gewisse potentielle Energie (man kann sich die potentielle Energie bezüglich des Punktes U denken, also den Level U als Potentialnullpunkt setzen).
Beim Abschwung nach unten, von A nach U, verliert der Körper potentielle Energie. Die Gesamtenergie bleibt jedoch erhalten, somit wird die abgebaute potentielle Energie in einen Zuwachs an kinetischer Energie "verwandelt": Der Körper wird schneller. (Dadurch steigt auch die benötigte Zentripetalkraft.)
c)
Punkt O:
ZO = m⋅vO 2 / r; dies soll gemäss Vorgabe gleich m⋅g sein. Es folgt:
vO = 3.1 m / s. Fadenkraft oben FO = 0 N.
Es braucht bei dieser Geschwindigkeit oben keine Fadenkraft, da bereits die Gewichtskraft allein die notwendige Zentripetalkraft aufbringt.
Kinetische Energie oben = m⋅vO 2 / 2 = 0.49 J.
Potentielle Energie oben bezüglich Potential-Null-Level U:
m⋅g⋅2r = 1.96 J.
Punkt U:
E kin, unten + E pot, unten = E kin, oben + E pot, oben ; dabei ist E pot, unten=0 J
Es folgt E kin, unten= 0.49 J + 1.96 J = 2.45 J = m⋅vU 2 / 2. Es folgt vU= 7.00 m/s.
ZU = FU - mg oder FU= ZU+ mg, deshalb FU= 5.88 N.
Punkt R:
Wir nehmen Epot,O bezüglich Potential-Null-Level R:
Ekin,R+ O J = Ekin,O+ Epot,O.
Ekin,R= 0.49 J + mgr = 1.47 J = m⋅vR 2 / 2. => vR= 5.42 m/s.
ZR = m⋅vR 2 / r = 2.94 N =FR
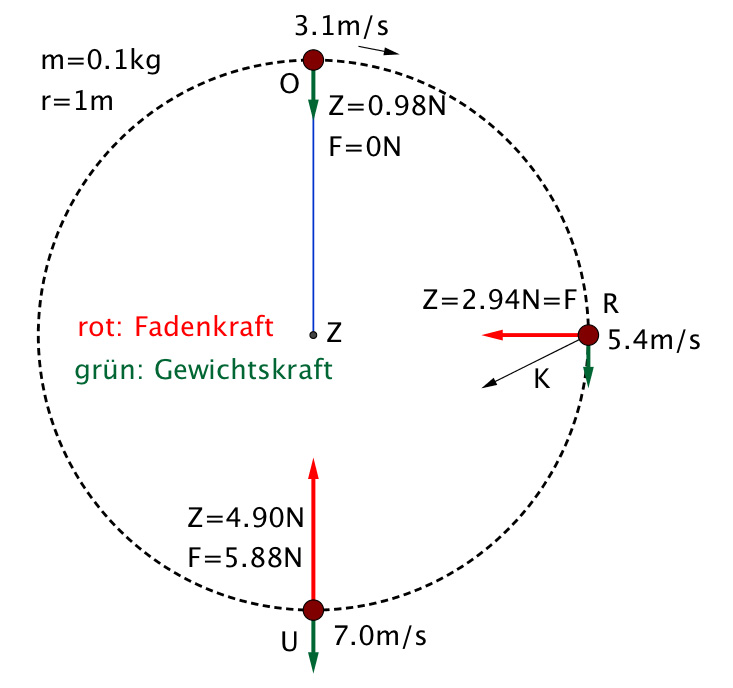
Die resultierende Kraft K beim Punkt R (Fadenzug vektoriell addiert mit Gewichtskraft) zeigt nach schräg links unten, d.h. der Körper wird in dieser Richtung beschleunigt. Das zeigt auch, dass die Geschwindigkeit zunimmt.
Die Kreisbewegung beim vertikalen Herumschwingen einer Masse setzt diese also verschiedenen Tempi und verschiedenen Zentripetalkräften aus. In einer Looping-Achterbahn treten an die Stelle der Fadenkräfte die Reaktionskräfte der Schienen. Unten sind die Zentripetalkräfte am grössten; die Zentripetalbeschleunigung in obigem Beispiel beträgt ca. 5g, was für eine Achterbahn viel zu viel wäre. Ein Achterbahnlooping muss unten deshalb weiter ausschwingen (grösserer Krümmungsradius).

Sanftes Ausschwingen eines Loopings
Aufgabe 46: Schwerpunkt

Wir denken uns den Koordinatenursprung (0/0) bei m1. Dann ist (Vektoren fett dargestellt)
rS = (m2/M) r12 + (m3/M) r13 .
Wählt man den Ursprung hingegen bei m2, so ist
rS= (m1/M) r21 + (m3/M) r23 .
Die Skizze links zeigt dies grafisch. Man sieht, dass die Grundseite des gleichseitigen Dreiecks im Verhältnis der Massenbruchteile gemessen an der Gesamtmasse M aufgeteilt wird. (Die Länge der Dreiecksseite ist 1.)
Man ziehe die gestrichelt gezeichneten Parallelen zu den Dreiecksseiten und erhält den Schwerpunkt S.
(Im gezeichneten Beispiel links verhalten sich die Massen an den Ecken wie 1 : 2 : 3.)
Merkwürdiges im Dreieck: siehe hier.
Aufgabe 47: Tiere in kalten Regionen

Antwort B, das grössere Tier.
Die Wärmeabstrahlung muss durch Nahrung kompensiert werden. Die Nahrungsmenge ist somit etwa proportional zur Oberfläche des Tieres. Nehmen wir an, das kleine Tier sei drei Mal kleiner als das grosse. Seine Oberlfäche ist dann neun Mal kleiner. Sein Eigengewicht ist aber 27 Mal kleiner. Es muss also im Verhältnis zu seinem Eigengewicht drei Mal mehr Nahrung aufnehmen als das grosse Tier und sich somit dauernd mit Fressen beschäftigen, was ein Problem werden kann. Das grosse Tier ist somit besser an die Kälte angepasst.
Vgl. dazu die Überlegungen von J.B.S. Haldane: On being the right size.
J.B.S. Haldane schreibt:
"For [that] reason small animals cannot live in cold countries. In the arctic regions there are no reptiles or amphibians, and no small mammals. The smallest mammal in Spitzbergen is the fox. The small birds fly away in winter (...). The most successful mammals are bears, seals and walruses.“