Würfelturnier

                   Die abgebildeten Würfel tragen nicht die gewöhnlichen Augenzahlen.

•             Der gelbe Würfel trägt die Augenzahlen 3, 3, 3, 3, 6, 6.
•             Der blaue Würfel trägt die Augenzahlen 1, 1, 5, 5, 5, 5.
•             Der grüne Würfel trägt die Augenzahlen 3, 4, 4, 4, 4, 5.
•             Der rote Würfel trägt die Augenzahlen    2, 2, 2, 6, 6, 6

                    Zwei Personen wählen je einen dieser Würfel aus und würfeln gegeneinander. Wer die höhere Augenzahl würfelt, gewinnt. -
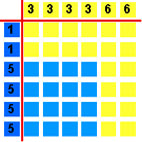
                    Es ist einleuchtend, dass dieses Spiel nicht sehr gerecht ist. Der gelbe Würfel ist ja gewiss "besser" als der blaue, wie folgende Gewinntabelle zeigt:
                    Blau gewinnt in 16, Gelb in 20 Fällen.

                     Welcher Würfel ist besser als der andere?

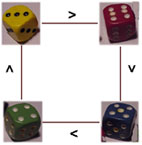
                     Man wird finden (y = yellow, r = red, b = blue, g = green):     y > r > b > g.

                      "Erstaunlicherweise" gilt jedoch    g > y.

                     Man hat ein zyklisches Schema:

                      Siehe auch: intransitive Würfel.

                      Ein zyklisches Schema liegt auch dem Kinderspiel "Schere, Stein, Papier" zugrunde: Schere > Papier > Stein > Schere.

                      (Schere schneidet Papier, Papier wickelt den Stein ein, Stein beschädigt die Schere.)
                      Die zyklische Ordnung befähigt dieses Spiel erst als Spiel zum Auslosen einer Gewinnperson!