Aussagenlogik
Der Inhalt der Aussagenlogik sind Aussagen, die entweder wahr oder falsch sein können. Die Aussagenlogik ist der gemeinsame Teil fast aller komplexerer Logiken.
1. Syntax der Aussagenlogik
Man hat einen Variablenvorrat V = {A, B, C, ... }. Daraus entstehen Formeln wie folgt:
- 0 und 1 sind Formeln.
- Jede Variable aus dem Vorrat V ist eine Formel.
- Sind φ und ψ Formeln, dann sind auch folgende Zeichenketten Formeln: ¬φ (Negation), φ∧ψ (UND-Verbindung, Konjunktion), φ∨ψ (ODER-Verbindung, Disjunktion), φ→ψ (Implikation), φ↔ψ (Äquivalenz), φ↮ψ (Antiäquivalenz).
Es gibt atomare, d.h. nicht weiter zerlegbare, Formeln sowie Teilformeln, die Teil einer andern Formel sind. Um Klammern zu sparen, definiert man:
Die Negation bindet am stärksten, dann folgen Konjunktion, dann Disjunktion und schliesslich, am schwächsten bindend, die Pfeile.
2. Semantik der Aussagenlogik
Enthält eine Formel n Variablen, A, B, C, ..., so kann jeder der n Variablen entweder der Wahrheitswert 0 oder 1 zugeordnet werden. Dies nennt man eine Belegung (oder Interpretation) der Formel. Damit können wir die Semantik (den "Inhalt") der Aussagenlogik definieren.
Wir definieren die Relation "Belegung I ist Modell für Formel ...", in Zeichen: |=, wie folgt:
- I |= 1 (I ist stets Modell für die Formel 1)
- I |≠ 0 (I ist nie Modell für die Formel 0)
- I ist Modell für eine Variable A genau dann, wenn die Belegung von A gleich 1 ist.
- I ist Modell für ¬φ genau dann, wenn I kein Modell für φ ist.
- I ist Modell für φ∧ψ genau dann, wenn I Modell für φ und Modell für ψ ist.
- I ist Modell für φ∨ψ genau dann, wenn I Modell für φ oder Modell für ψ ist.
- I ist Modell für φ→ψ genau dann, wenn I nicht Modell für φ oder I Modell für ψ ist.
- I ist Modell für φ↔ψ genau dann, wenn I Modell für φ→ψ und I Modell für ψ→φ ist.
- I ist Modell für φ↮ψ genau dann, wenn I nicht Modell für φ↔ψ ist.
3. Wahrheitstafeln für die Darstellung der verschiedenen Belegungen
Schaltalgebra: Seien im Folgenden A und B Formeln (wir haben oben Formeln mit griechischen Buchstaben bezeichnet, wechseln nun aber der Einfachheit halber zu lateinischen, fetten Buchstaben). Zu den Formeln (Aussagen) A und B können wir uns je einen Schalter vorstellen: Stellung oben bedeute "1", Stellung unten bedeute "0". Die folgenden Verknüpfungen lassen sich dann durch Schaltungen nachbilden. Die Resultat-Spalte wird durch ein Lämpchen, das brennt (1) oder nicht brennt (0) dargestellt.
| A | ¬A |
| 0 | 1 |
| 1 | 0 |
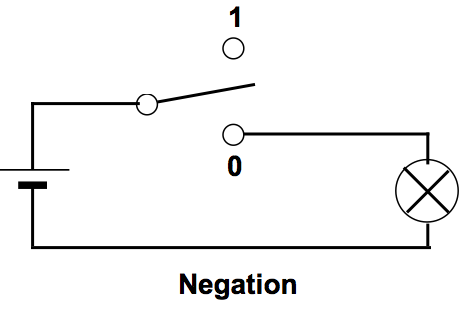
Negation.
Schaltung: Verkehrter Schalter: Stellung unten (0): Strom fliesst, Stellung oben (1): Strom unterbrochen.
| A | B | A∧B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Konjunktion:
Schaltung: Zwei hintereinander angeordnete Schalter.
| A | B | A∨B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Disjunktion (oder Adjunktion):
Schaltung: Zwei parallel angeordnete Schalter.
| A | B | A→B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
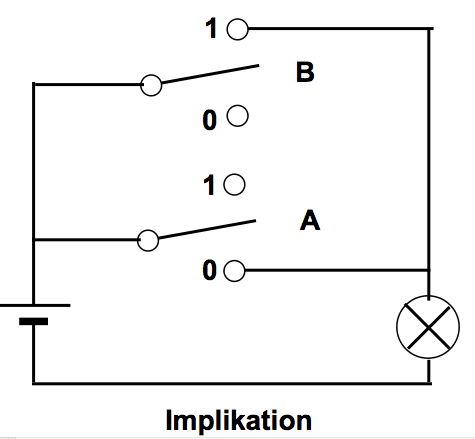
Implikation:
Ein verkehrter Schalter (¬A) und ein normaler Schalter (B) sind parallel angeordnet
(vgl. die Äquivalenz von A → B mit ¬A ∨ B).
Bild: Nur wenn Schalter A auf 1 UND Schalter B auf 0 steht, bleibt das Lämpchen dunkel.
| A | B | A↔B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Äquivalenz
(Wie sähe eine Schaltung hierfür aus?)
| A | B | A ↮ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Antiäquivalenz
Bemerkung zur Implikation
| A | B | A→B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Die Implikation "A impliziert B" oder "B folgt aus A" deckt sich nicht unbedingt mit dem, was wir anschaulich darunter verstehen. Wir können uns jedoch die Definition durchaus etwas plausibel machen.
Nehmen wir für A die Aussage: "Ich giesse die Blume."
Für B wählen wir die Aussage: "Die Blume wird nass."
Erste Zeile der Tabelle oben: Ich giesse nicht; die Blume wird nicht nass: Kann zutreffen.
Zweite Zeile: Ich giesse nicht; die Blume wird nass: Kann zutreffen, denn die Blume kann auch durch andere Einflüsse nass werden (Regen, Tau).
Dritte Zeile: Ich giesse die Blume; sie wird nicht nass: Das kann nicht zutreffen, denn eine Folge des Giessens ist das Nasswerden.
Vierte Zeile: Ich giesse; die Blume wird nass: Trifft zu, wenn ich giesse.
Das Wesentliche der Implikation liegt also in der dritten Zeile: (1 ; 0) ↦ 0 ist zwingend.
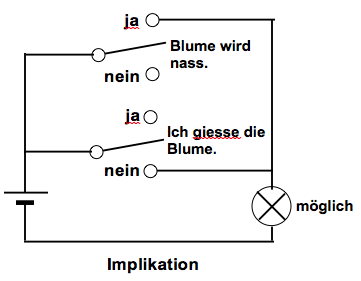
Einzig bei "Ich giesse: ja" UND "Blume nass: nein" bleibt das Lämpchen dunkel, denn dies ist unmöglich.
Zur Äquivalenz von A → B mit ¬A ∨ B:
| A | B | A→B | ¬A | ¬A∨B |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
Man sieht, dass dieselben Belegungen dasselbe Resultat erzeugen. Oder anders gesagt: Jedes Modell für A→B (Zeilen 1, 2, 4) ist auch Modell für ¬A∨B (ebenfalls Zeilen 1, 2, 4) und umgekehrt.
Noch eine Bemerkung zur Implikation
Quelle: Paul Hoyningen-Huene: Formale Logik, Reclam, Stuttgart 1998, p.50
Die Implikation ist nicht einfach die alltägliche "Wenn-Dann-Verknüpfung", denn diese ist teilweise vom inhaltlichen Sinn der Aussagen abhängig.
Wir erwarten im Alltag ja geradezu einen inhaltlichen Zusammenhang zwischen dem Wenn- und dem Dann-Teil.
"Wenn es morgen schneit, dann fahre ich in die Berge."
Eine eindeutige Wahrheitstabelle lässt sich hier nicht errichten. Was, wenn es nicht schneit? Was tue ich dann?
Einzig der Fall, dass A: "Es schneit morgen" richtig und B: "Ich fahre in die Berge" falsch ist, ist eindeutig auszuschliessen, wenn ich obige Absicht fest geäussert habe.
Das ist in der Wahrheitstafel die dritte Zeile (siehe Spalte rechts):
| A | B | A→B |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Und genau diese vom Inhalt unabhängige Zeile bildet die Basis für die Definition der Implikation, nämlich so: A ∧¬B ist falsch, d.h. ¬(A ∧¬B) = ¬A∨B ist richtig (die letzte Gleichheit ergibt sich aus dem Gesetz von de Morgan).
Und dieses (¬A∨B) kann man als Definition für A→B wählen.
Dann füllt sich die Tabelle wie gehabt:
| A | ¬A | B | A→B = ¬A∨B |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
Zeige: (A→B) ↔ (¬A∨B):
| A | B | A→B | ¬A∨B | (A→B) ↔ (¬A∨B) |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Wir sehen, dass die Äquivalenz (A→B) ↔ (¬A∨B) allgemeingültig (tautologisch) ist, unabhängig von den Belegungen von A und B.
Solche Äquivalenzen zeigen, dass wir eigentlich mit weniger Symbolen auskommen. Wir können uns z.B. auf die Symbole ¬ und → beschränken.
So ist etwa wegen obiger Äquivalenz A ∨ B gleichwertig zu ¬A → B.
4. Logische Folgerung
Sei die Menge M eine Menge von aussagenlogischen Formeln. Sei ψ ebenfalls eine aussagenlogische Formel.
Wenn jedes Modell der Elemente von M auch ein Modell von ψ ist, schreiben wir:
M |= ψ, d.h. M impliziert ψ.
Ist M die leere Menge, schreiben wir: |= ψ ; dann ist ψ allgemeingültig.
Ein Beispiel:
| A | B | A∧B | B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Jedes Modell von A∧B ist auch ein Modell von B, d.h. wenn in der Wahrheitstabelle oben bei A∧B eine 1 steht, dann steht auch bei B in derselben Zeile eine 1.
Das heisst: B folgt logisch aus A∧B. Die Umkehrung gilt jedoch nicht, wie die Tabelle (2. Zeile) zeigt.
Übungen
Man zeige auf der semantischen Ebene, d.h. mittels Wahrheitstafeln
a) A ∧ ¬A → B (ex contradictione quodlibet, aus einem Widerspruch folgt Beliebiges)
b) A ∧ B → C ↔ A → (B → C) ("Deduktionstheorem", s. unten)
In Worten: "Unter Voraussetzung A UND B wird C deduziert" ist gleichwertig mit:
"Aus A wird deduziert, dass aus B die Deduktion auf C gilt." Dies ist weiter unten der
Inhalt des Deduktionstheorems.
Lösung b)
| A | B | C | A ∧ B | A ∧ B → C | B → C | A → (B → C) |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Die grünen Spalten sind zeilenweise gleich, was die Äquivalenz zeigt.
5. Der formale Kalkül der Aussagenlogik
Wir gehen aus von Axiomen und wollen daraus (mittels Schlussregeln) genau die allgemeingültigen Formeln herleiten. Wir arbeiten ohne inhaltlichen Bezug rein auf der formalen Ebene. Wir vergessen also die ganze Semantik mit den Wehrheitstafeln und arbeiten einzig mit inhaltslosen Axiomen und Regeln.
Wir können dann sagen: Unsere Schlüsse sind korrekt. Von wahren Schlüssen sollten wir nicht sprechen, wahr sind Aussagen; "wahr" ist ein Begriff aus der Semantik, "korrekt" ein Begriff, der sich auf die formalen Schlüsse im Kalkül bezieht.
Der Einfachheit halber wählen wir für Aussagen wieder lateinische fette Buchstaben.
Axiome
A1: A → (B → A): Abschwächungsregel.
Hinter A darf ich "→ (B → A)" -mit einer grammatikalisch korrekten Aussage B- setzen. Etwas salopp formuliert: Jede Aussage A impliziert ihre Sukzedensfähigkeit mit (beliebigem) Antezedens B.
A2: (A → (B → C)) → ((A → B) → (A → C)): Distributivgesetz für →
A3: (¬B → ¬A) → (A → B): Kontraposition.
"Wenn Boden nicht benetzt (¬B), dann Boden nicht nass (¬A) impliziert: Wenn Boden nass (A), dann Boden benetzt (B)."
Umkehrung der Schlussrichtung beim Übergang zu den Negationen.
Einzige Schlussregel: Modus ponens (Abtrennungsregel)
A
A
→ B
--------
B
B ist beweisbar, wenn A beweisbar ist und A die Aussage B impliziert.
Ganz formal gedacht: Wenn in irgend einer Zeile einer formalen Ableitung die Formel A steht und in einer andern Zeile
A → B, dann darf ich in einer weiteren Zeile B notieren.
Bemerkung zum Axiom 1:
Wir arbeiten im abstrakten Kalkül rein formal-syntaktisch. Trotzdem können wir einen kurzen semantischen Abstecher machen und zeigen, dass Axiom 1 als "allgemeingültige Basis" gerechtfertigt ist. Wir betrachten dazu die folgende Wahrheitstabelle:
| A | B | B→A | A →(B→A) |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Die Schluss-Spalte zeigt nur Einsen. Mit Wahrheitstabellen sind wir jedoch im Bereich der semantischen Wahrheit. Dieser Begriff ist verschieden vom Begriff der syntaktischen Beweisbarkeit. Axiom 1 wird einfach formal gesetzt. Im formalen System können wir nicht mit Wahrheitstabellen arbeiten, sondern nur mit den Axiomen und der Schlussregel des Modus ponens.
Bemerkung zur Schlussregel
Neben dem Modus ponens (s. oben) gibt es noch den Modus tollens, der so geht:
¬B
A → B
--------
¬A
Der Modus tollens ist die Grundlage der sogenannten Falsifikation: Wenn B aus A folgt, B jedoch nicht zutrifft, trifft auch A nicht zu, d.h. A wird durch ¬B falsifiziert.
Formal: ((A → B)∧¬B) → ¬A.
Die Wahrheitstabelle ergibt wiederum keinen Beweis, zeigt jedoch, dass im semantischen Bereich obige Formel allgemeingültig ist:
| A | B | A → B | ¬B | (A → B)∧¬B | ¬A | ((A → B)∧¬B) → ¬A |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Die Formel muss (und kann auch) rein formal hergeleitet (bewiesen) werden.
Bemerkung zum Auseinanderklaffen von "Wahrheit" und "formaler Ableitbarkeit":
A →(B→A) ist in der Semantik der Wahrheitstafeln allgemein wahr. Diese Einsicht hat, wie man sieht, mit dem formalen Kalkül der Aussagenlogik nichts zu tun; sie erfolgt via Ausfüllen der Wahrheitstafeln gemäss der Interpretation des Implikationspfeils.
Dass A →(B→A) auch im formalen Kalkül vorkommt, muss jedoch rein formal gezeigt werden.
Im konkreten Fall wird A →(B→A) einfach axiomatisch gesetzt und damit in den Kalkül aufgenommen. Ohne diesen Schritt könnte A →(B→A) formal nicht hergeleitet werden, wäre aber im semantischen Bereich der Wahrheitstafeln trotzdem wahr: Der Kalkül wäre dann unvollständig.
Der Vollständigkeitssatz bezüglich Aussagen- und Prädikatenlogik besagt, dass jede allgemeingültig wahre Aussage auch im entsprechenden Kalkül hergeleitet werden kann.
Für komplexere Systeme, welche die Zahlentheorie enthalten, wird dies prinzipiell nicht mehr gelten.
Das Auseinanderklaffen von Wahrheit und formaler Ableitbarkeit ist dem "normalen" Leben nicht so fremd, wie wir vielleicht meinen. Man denke etwa an juristische Beweisverfahren: Eine Tat kann in Wahrheit begangen worden sein, das juristisch-formal korrekte Beweisverfahren kann eventuell diese Tat nicht nachweisen, da sich die Rechtssprechung auf genau definierte formale Grundsätze verlassen muss.
Das Erstaunen, dass Ähnliches auch in der Mathematik auftreten kann, rührt vielleicht von der verbreiteten, aber falschen Ansicht her, dass die Mathematik auf einer einzigen Ebene stattfindet und man fälschlicherweise logisch-semantische Folgerung |= und formal-syntaktische Ableitbarkeit |- vermischt. Tatsächlich muss man aber auch in der Mathematik -wie in der Jurisprudenz- eine semantische und eine formal-syntaktische Ebene unterscheiden.
Beim mathematischen Folgern befinden wir uns in der semantischen Ebene: Wir sprechen über gewisse Objekte: Zahlen, Figuren, Mengen, Funktionen. Dem logischen Formalismus sind solche Begriffe "egal".
Wir können jedoch auch den inhaltsleeren Formalismus zum Inhalt unserer Betrachtungen machen: Dann sprechen wir über den Formalismus als Objekt. Dadurch treten wir jedoch aus dem Formalismus heraus und hinein in eine inhaltliche Metaebene.
Wenn wir etwa zeigen, dass eine Formel im betrachteten Formalismus nicht ableitbar ist (ein "Nicht-Satz" ist), zeigen wir dies im semantischen Bereich. (Ein einfaches Beispiel liefert Douglas R. Hofstadter in "Gödel, Escher, Bach", 1. Aufl. 2004, mit seinem MIU-Formalismus: Um zu zeigen, dass MU ein Nicht-Satz ist, muss man aus dem Formalismus heraustreten und Zahlen einbeziehen.)
Um den Formalismus zu programmieren, muss man ebenfalls aus ihm heraustreten. Die Programmier-Überlegung für den Modus ponens wäre etwa: Steht in einer Zeile A und in einer andern Zeile A→B, so notiere in einer weiteren Zeile B. (Man benötigt "If-then"- und "AND"-Überlegungen.)
Einschub 1: Der M I U-Formalismus von Douglas R. Hofstadter aus: "Gödel, Escher, Bach".
Alphabet: M, I, U. Daraus werden "Wörter" gebildet.
Mit x sei ein beliebiges bisher abgeleitetes Wort gemeint. x gehört nicht zum Formalismus.
Axiom (Ausgangswort): M I
Regeln:
1. Aus x I kann x I U gebildet werden.
2.
Aus M x kann M x x gebildet werden.
3. I I I kann durch U ersetzt werden.
4. U U kann man streichen.
Aufgabe: Bilden Sie M U.
Lösung:
Nach längerem Probieren wird man erfolglos aufgeben. M U will einfach nicht gelingen. Man vermutet: M U ist nicht ableitbar, d.h. ist ein "Nicht-Satz" des Formalismus.
Was eine Metabetrachtung bringt:
Behauptung: Die Anzahl der Buchstaben I in einem Satz kann nie ein Vielfaches von 3 und somit auch nie 0 werden.
Ad hoc-Definition: Sei ein Satz, in dem die Anzahl der Buchstaben I kein Vielfaches von 3 ist ein E-Satz genannt (E für Eigenschaft).
Begründung:
M I ist ein E-Satz. Regel 2 (Verdoppelung der Anzahl I) und Regel 3 (Verminderung der Anzahl I um 3) erzeugen aus einem E-Satz wieder einen E-Satz. Regeln 1 und 4 ändern an der Anzahl I nichts und erzeugen aus einem E-Satz erneut einen E-Satz.
D.h. keine der Regeln kann aus einem E-Satz einen Nicht-E-Satz erzeugen: E wird vererbt.
Der Start M I ist ein E-Satz. Also sind nach obigen Überlegungen zu den vier Regeln alle Sätze E-Sätze. Man kann also nie alle I durch Regel 3 streichen und wegbringen: In jedem Satz kommt ein Buchstabe I vor. Deshalb ist M U nicht zu erreichen und ist kein Satz des Formalismus.
Einschub 2:
Ein "Gödel-Code" zum M I U - Formalismus
Hofstadter ordnet jedem Buchstaben eine "Gödelzahl" zu:
M ↔ 3; I ↔ 1; U ↔ 0.
Jeder Satz wird dann als Zahl codiert. Beispiel:
MI ↔ 31; M U I ↔ 301; M U I U U I U ↔ 3010010
Nun können zahlentheoretische Überlegungen greifen (Beispiel: Die Quersumme dieser Zahlen ist nie durch 3 teilbar. Das "zeigt" erneut, dass M U ↔ 30 kein Satz ist).
Fazit:
Der Formalismus kann aus sich heraus nicht ableiten, dass M U kein Satz des Formalismus ist. Dazu ist eine zahlentheoretische Metabetrachtung nötig, in welcher der Formalismus ein Untersuchungsobjekt wird: Wir gelangen in den Bereich der normalen semantischen Mathematik. (Die Gödelzahl 30 im Beispiel links sagt uns, dass M U kein Satz des M I U - Formalismus ist.)
Den Sätzen des M I U -Formalismus Gödelzahlen zuzuordnen, ist noch nichts Aufsehen Erregendes. Gödel tat etwas viel "Verrückteres": Er ordnete den Sätzen der "Zahlentheorie" (dem Theorie-System der natürlichen Zahlen) sogenannte "Gödelzahlen" zu (ähnlich dem Beispiel links, jedoch viel raffinierter), wodurch die Zahlentheorie gewissermassen sich selber "betrachten" kann. Die Gödelzahlen sind einerseits gewöhnliche Elemente der Theorie der natürlichen Zahlen, stehen andererseits aber auch für Sätze dieser Theorie, sind also gewissermassen dann Betrachter der Theorie. Sie wirken so auf zwei verschiedenen Ebenen.
Dadurch gelang Gödel folgendes: Er konnte eine Aussage G der "Zahlentheorie" konstruieren, die via die zugeordnete Gödelzahl über sich selber sagen konnte: Ich bin kein Satz der Zahlentheorie, d.h. ich kann darin nicht formal hergeleitet werden.
Was heisst das nun? Ist G nun ein Satz der Theorie oder nicht?
Die Antwort "Ja" geht nicht, denn jeder formal abgeleitete Satz ist (Korrektheit des Kalküls vorausgesetzt) automatisch wahr, d.h. die Aussage "Ich bin kein formal abgeleiteter Satz" wäre wahr im Widerspruch zu unserem "Ja". (Gödel bewies mehr als diese semantische Version, welche die Korrektheit des Kalküls voraussetzt.)
G ist also nicht ableitbar, das ist jedoch das, was G behauptet, also ist G semantisch wahr.
Semantisch wahren Aussagen entsprechen jedoch arithmetisch wahre Formeln. Wir haben also eine wahre Formel gefunden, die formal nicht herleitbar ist.
Übrigens ist auch ¬G im Kalkül nicht ableitbar, da wegen "G wahr" ¬G falsch ist, und falsche Sätze können formal nicht abgeleitet werden. Sowohl G wie auch ¬G sind also nicht ableitbar: G ist unentscheidbar.
Dies führte Gödel zu seinem Unvollständigkeitssatz für Systeme, die reich genug sind, die Theorie der natürlichen Zahlen zu enthalten.
Beispiel einer formalen Ableitung
(Quelle: Dirk W. Hoffmann, Grenzen der Mathematik, Spektrum 2011, p. 94)
Behauptung: Wir leiten die Allgemeingültigkeit der Aussage φ: A → A ab.
1. |- A → ((A → A) → A); Axiom 1
2. |- (A → ((A → A) → A)) → ( (A → (A → A)) → (A → A)); Axiom 2
3. |- (A → (A → A)) → (A → A); Modus ponens auf Schritt 1 und 2 angewendet
4. |- A → (A → A); Axiom 1
5. |- A → A; Modus ponens auf Schritt 3 und 4 angewendet
Das Zeichen |- bedeutet: "beweisbar im Kalkül".
Man vergleiche dazu auf der semantischen Ebene die folgende Wahrheitstabelle:
| A | A → A |
| 0 | 1 |
| 1 | 1 |
A → A ist (semantisch) allgemeingültig: |= A → A.
Die Herleitung via Wahrheitstafel ist jedoch etwas Anderes als die formal-syntaktische Ableitung durch die Kalkülregeln (links).
Die Vollständigkeit des Aussagenkalküls besagt, dass jede allgemeingültige (tautologische) Aussage eine formal-syntaktische Beweiskette besitzt: Der Kalkül ist wirklich "gut gemacht":
Aus |= folgt |-.
6. Das Deduktionstheorem
Für beliebige aussagenlogische Formeln A , A₁, ..., An und B gilt:
{A, A₁, ..., An} |- B ⇔ {A₁, ..., An} |- A → B
Speziell für {A₁, ..., An} = { } ergibt sich { A } |- B ⇔ |- A → B
Die Richtung von rechts nach links lässt sich sofort mithilfe des Modus ponens zeigen. Die Richtung von links nach rechts ist etwas schwieriger herzuleiten.
Das Deduktionstheorem in Worten:
Folgende Aussagen sind äquivalent:
(i): Unter der Voraussetzung {A, A₁, ..., An} ist B beweisbar.
⇔
(ii): Unter der Voraussetzung {A₁, ..., An} ist die Implikation A → B beweisbar
(A wird aus den Voraussetzungen entfernt und ins Antezedens der Implikation verlagert).
Beweis-Idee für die Richtung von links nach rechts:
Der alte Beweis (linke Seite des Theorems) habe m Zeilen z1, ..., zm -1, zm=B.
Wir erzeugen die neuen Zeilen [ ... ], (A →z1), [ ... ], ..., [ ... ], (A →zm -1), [ ... ], (A→B).
Um zu zeigen, dass dies für jedes zi möglich ist, müssen wir 3 Fälle unterscheiden:
(i): zi ist ein Axiom.
(ii):
zi ist A selber.
(iii):
zi entstand aus zj und zj→zi via Modus ponens, d.h. weiter oben gab es zwei Beweiszeilen A→zj und A→(zj→zi).
In jedem der drei Fälle können wir die Beweisidee, aus zi die Zeile A → zi herzustellen, verwirklichen.
Fall (i): zi ist ein Axiom:
|- zi
|- zi → (A → zi) (Axiom 1)
|- A → zi (Modus ponens)
Fall (ii): zi ist A selber:
Wir haben oben (Schluss von Abschnitt 5: "Beispiel einer Ableitung", hellblauer Kasten)
|- A → A hergeleitet.
Fall (iii): zi wurde aus zj und zj → zi via Modus ponens erzeugt. Dann gibt es weiter oben im Beweis die Zeilen
|- A → zj und
|- A → (zj → zi). Wir fahren so weiter:
|- A → (zj → zi) → ( (A → zj) → (A → zi) ) (Axiom 2)
|- (A → zj) → (A → zi) (Modus ponens)
|-
A → zi (Modus ponens)
Beispiel der Anwendung des Deduktionstheorems in einem Beweis
Satz:
¬A → (A → B)
Beweis:
1. Axiom 1: |- ¬A → (¬B→ ¬A)
2. Deduktionstheorem ⇐: { ¬A } |- ¬B → ¬A
(Auslagern der Antezendenz in die Voraussetzungen)
3. Axiom 3: |- (¬B → ¬A) → (A → B)
4. Modus ponens auf Schritte 2 und 3: { ¬A } |- (A → B)
5. Deduktionstheorem ⇒: |- ¬A → (A → B)
(Wieder Einlagern der Voraussetzung in die Antezedenz)
Eine Folgerung aus dem Satz links:
Mit dem Satz ¬A → (A → B) und dem Modus ponens gilt das Folgende:
Wäre innerhalb des Kalküls ein Widerspruch herleitbar (A und ¬A), so folgte aus obiger Behauptung via ¬A plus Modus ponens A → B.
Aber auch A wäre ableitbar, sodass aus A → B via A plus Modus ponens B folgte.
B ist aber irgend eine Aussage.
In einem widersprüchlichen Kalkül liessen sich also alle Aussagen beweisen, d.h. jede Formel wäre ein Theorem (ex contradictione quodlibet: aus einem Widerspruch folgt Beliebiges).
Deshalb will man widerspruchsfreie Systeme haben.
7. Eigenschaften des Kalküls der Aussagenlogik
Semantische Eigenschaften:
- Alle Axiome sind allgemeingültig (für Axiom 1 haben wir dies mithilfe einer Wahrheitstabelle oben bereits gezeigt). Der Modus ponens ist zudem allgemeingültigkeits-erhaltend. Folglich ist jedes formal hergeleitete Theorem auch allgemeingültig wahr, d.h. aus |- folgt |=: Der Kalkül ist korrekt. (Wir haben ihn "gut" konstruiert.)
- Es lässt sich auch die Umkehrung zeigen: Jede allgemeingültige Formel ist auch herleitbar: Der Kalkül ist auch vollständig (aus |= folgt |-). Diese Umkehrung ist nicht selbstverständlich und viel schwieriger zu zeigen (Gödelscher Vollständigkeitssatz, 1928).
Syntaktische Eigenschaften:
- Ein korrekter Kalkül ist auch stets widerspruchsfrei, d.h. es kann mit A nicht auch noch ¬A hergeleitet werden, da nicht zugleich A und ¬A wahr sein können.
- Der Kalkül ist nicht negationsvollständig, d.h. es gibt Formeln A, für die weder A noch ¬A aus den Axiomen abgeleitet werden können, d.h. aus der Nichtableitbarkeit von ¬A folgt nicht die Ableitbarkeit von A.
Zur Widerspruchsfreiheit eines Kalküls
Wenn zu einem Kalkül ein Modell gefunden werden kann, das jedes abgeleitete Theorem in eine wahre Aussage im Modell überführt, ist der Kalkül widerspruchsfrei.
Beispiel (s. Nagel: Der Gödelsche Beweis, Oldenbourg 2001):
Seien zwei Klassen, S und E, gegeben. Axiome:
1. Zwei beliebige Elemente von E sind genau in einem Element von S enthalten.
2. Kein Element von E ist in mehr als zwei Elementen von S enthalten.
3. Die Elemente von E sind nicht alle in einem einzigen Element von S enthalten.
4. Zwei beliebige Elemente von S enthalten genau ein Element von E.
5. Kein Element von S enthält mehr als zwei Elemente von E.
Ist das System widerspruchsfrei?
Antwort:
Wir nehmen folgendes Modell:
Wir betrachten ein Dreieck. E sei die Menge der Ecken, S die Menge der Seiten.
"e ist in s enthalten": Ecke e liegt auf Seite s.
Das Modell zeigt die Widerspruchsfreiheit der fünf Bedingungen, denn es zeigt die Korrektheit, und ein korrekter Kalkül ist widerspruchsfrei.
Ein kurzer Überblick: hier
Eine ausserordentlich gute Einführung: Armin P. Barth: Beweisen ohne Sorgen.
8. Vorbemerkungen
Warum genügt die Aussagenlogik allein für mathematische Zwecke nicht?
Nehmen wir das bereits ziemlich abgedroschene Beispiel:
Alle Menschen sind sterblich.
Sokrates ist ein Mensch.
------------------------------------
Sokrates ist sterblich.
Diesen Schluss kann die Aussagenlogik gar nicht vollziehen, denn in ihrem formalen Kleid sähe der obige Dreizeiler so aus: (r ∧ s) → t. Diese Formel ist jedoch keine logische Wahrheit. Für die Gültigkeit des Schlusses ist wesentlich, dass "Mensch", "sterblich" und "Sokrates" je zwei Mal auftreten. In der Aussagenlogik kann jedoch eine Aussage ("Sokrates ist ein Mensch") nicht in Subjekt ("Sokrates") und Prädikat ("ist ein Mensch") aufgespalten werden. Kurzschreibweise: Ma. M steht für "ist ein Mensch" und a steht für "Sokrates"; das Prädikat M wird zuerst notiert, dann folgt das Argument a.
Die Aussagenlogik muss also erweitert werden auf Aussagen, die ein logisches Subjekt und ein logisches Prädikat enthalten, z.B. "Sokrates" (Subjekt) "ist ein Mensch" (Prädikat).
Die Begriffe logisches Subjekt und logisches Prädikat sind, wie das Beispiel zeigt, nicht deckungsgleich mit den grammatikalischen Begriffen Subjekt und Prädikat. Das Subjekt ist das, worüber man etwas aussagt, das Prädikat ist das, was über das Subjekt ausgesagt wird.
Es gibt ein- und mehrstellige Prädikate:
b ist Tochter von a: "ist Tochter von" ist zweistellig; man muss zwei "Werte", b und a, einsetzen.
Kurzschreibweise: Tba. T steht für "Tochter von". Das Prädikat T wird zuerst notiert, anschliessend folgen die Argumente b und a (in dieser Reihenfolge!).
a und b sind Individuenkonstanten.
Prädikate sind Relationen (ein- oder mehrstellige).
Noch zwei in der Philosophie oft benutzte Begriffe:
Intension eines Prädikats: Der Sinn, die Bedeutung.
Extension eines Prädikats: Die Menge der Individuen, auf die das Prädikat zutrifft.
Beispiel in Bezug auf Dreiecke: "gleichwinklig" und "gleichseitig": Intension verschieden, Extension gleich.
Quantoren:
alle: ∀: Allquantor. Er wird zusammen mit einem Individuenbereich verwendet: "Für alle x aus einem bestimmten Individuenbereich gilt..."
x wird dabei als durch den Quantor gebundene Variable bezeichnet, Variable deshalb, weil x den ganzen Individuenbereich durchläuft.
Für die leere Individuenmenge U sei die Aussage "für alle x aus
U gilt ..." wahr.
Es existiert: ∃: Existenzquantor: "Im betrachteten Individuenbereich existiert mindestens ein x mit der Eigenschaft ..."
Auch hier ist die Variable x durch den Quantor gebunden.
Nicht durch Quantoren gebundene Variable heissen frei.
In einer prädikatenlogischen Formel kommen vor:
Individuenvariablen x, y, z, ...
Individuenkonstanten a, b, c, ...
Prädikatbuchstaben A, B, C, ...
Quantoren
Junktoren
Klammern
9. Prädikatenlogische Formeln (Ausdrücke)
Das Alphabet einer Sprache erster Stufe umfasst diese Zeichen:
- Variablen x, y, z, ...
- Junktoren ¬, ∧ , ∨, →, ↔
- Quantoren ∀, ∃
- das Gleichheitszeichen ≡
- Klammersymbole ), (
- einer Menge von Relationssymbolen P, Q, R, ... (1- bis m-stellig)
- eine Menge von Funktionssymbolen f, g, h, ... (1- bis n-stellig)
- eine Menge von Konstanten
Die unter den ersten fünf Punkten genannten Zeichen bilden die Menge Α und die unter den letzten drei Punkten genannten Elemente bilden die Symbolmenge S. S kann leer sein.
A ∪
S ist das Alphabet der Sprache erster Stufe, S ihre Symbolmenge.
Beispiel einer Symbolmenge: Die Symbolmenge der Gruppentheorie ist { ο, e } (Verknüpfungsoperator ο und Zeichen e fürs Neutralelement).
Wir definieren bei gegebenem Alphabet die S-Terme (Termkalkül):
- Jede Variable ist ein S-Term.
- Jede Konstante aus S ist ein S-Term.
- Sind t1, ... , tn S-Terme und ist f ein n-stelliges Funktionssymbol, so ist auch ft1, ... , tn ein S-Term.
Die Menge der S-Terme wird mit TS bezeichnet.
Nun definieren wir, was ein S-Ausdruck (eine S-Formel) ist (Ausdruckskalkül):
Man erzeugt S-Ausdrücke durch endliche Anwendung folgender Regeln:
- Für S-Terme t1 , t2 ist t1 ≡ t2 ein S-Ausdruck.
- Sind t1, ... , tn S-Terme und R ein n-stelliges Relationssymbol aus S, so ist Rt1, ... , tn ein S-Ausdruck.
- Sind φ und ψ S-Ausdrücke und x eine Variable, dann sind auch ¬φ, φ∧ψ , φ∨ψ, φ→ψ, φ↔ψ, ∀xφ, ∃xφ S-Ausdrücke.
Die unter den ersten beiden Punkten genannten Ausdrücke heissen atomar.
Für Ausdrücke verwendet man meist griechische Buchstaben (hier werden gelegentlich fette lateinische Grossbuchstaben verwendet).
Die Menge der S-Ausdrücke wird mit LS bezeichnet. LS heisst die zur Symbolmenge S gehörende Sprache erster Stufe oder Sprache der Prädikatenlogik erster Stufe.
Satz: Terme und Ausdrücke können eindeutig in die Terme und Ausdrücke zerlegt werden, aus denen sie entstanden sind.
Die Funktion var ordnet jedem S-Term t die Menge var(t) der in ihm vorkommenden Variablen zu. Die Funktion TA ordnet jedem S-Ausdruck die Menge seiner Teiilausdrücke zu.
Es gibt freie und an einen Quantor (∃,∀) gebundene Variable.
10. Prädikatenlogische Interpretation
Eine prädikatenlogische Interpretation (S-Struktur) besteht aus einer nichtleeren Menge U ("Universum", Grundbereich, Individuenbereich, Träger) und einer Abbildung I, die jedem n-stelligen Funktionssymbol f eine Funktion I(f): Uⁿ → U, jedem n-stelligen Relationssymbol P eine Relation I(P)⊂Uⁿ und jeder Konstanten c aus S ein Element I(c) aus U zuordnet.
Die Variablen werden durch eine Belegung interpretiert. Eine Belegung ordnet jeder Variablen vn eine Variable aus U zu.
Eine Interpretation (U, I) macht also die Symbole innerhalb des gewählten Universums via I lebendig.
Beispiel (Quelle: Heinz-Dieter Ebbinghaus, Jürg Flum, Wolfgang Thomas: Einführung in die mathematische Logik, Springer 2018, 6. Auflage, p.27):
Sei R ein zweistelliges Relationssymbol. Wir betrachten die Zeichenreihe ∀v0Rv0v0.
Nun interpretieren diese Reihe: Grundbereich sei die Menge der natürlichen Zahlen. R interpretieren wir als "teilt". Die abstrakte Zeichenfolge erhält dann folgende Interpretation: Für jede natürliche Zahl v gilt: v teilt v. In dieser Interpretation gilt der Ausdruck ∀v0Rv0v0. Die Interpretation erfüllt die Formel.
Ändern wir die Interpretation: Grundbereich ganze Zahlen; R interpretiert als <, dann gilt
der Ausdruck in dieser Interpretation nicht. (Für jede ganze Zahl v gilt: v < v: dies ist falsch.) Die Interpretation erfüllt die Formel nicht.
Mit solchen Interpretationen der Zeichenketten begeben wir uns in den Bereich der Bedeutung, der Semantik.
Ein weiteres Beispiel (aus Paul Hoyningen-Huene, Formale Logik, Reclam 1998, p. 212):
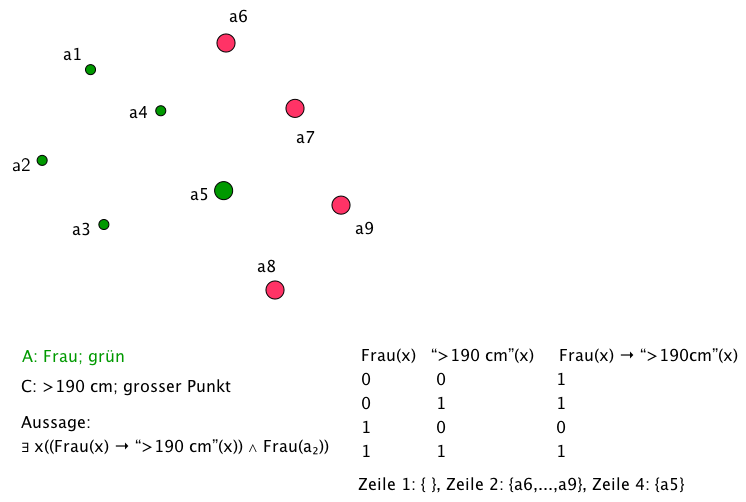
Die Formel φ laute: ∃x ((Ax → Cx) ∧ Aa)
Wir interpretieren diese Formel wie folgt:
U bestehe aus 9 Elementen: U = {a1, ... , a9}.
Dem Individuenbuchstaben a werde
a2 zugeordnet.
Dem Prädikatsymbol A sei die Menge {a1, ... , a5} als Relation zugeordnet. Das bedeutet, dass Aa1, ... , Aa5 wahr sind. Wir bezeichnen das interpretierte Prädikat mit AI (I stehe für "interpretiert").
Dem Prädikatsymbol C sei
{a5, ... , a9} zugeordnet.
Mehrstellige Prädikate sind in diesem Beispiel nicht vorhanden.
Jetzt soll obiger Formel φ ein Wahrheitswert zugeordnet werden.
Zunächst ist AIa2 wahr, denn a2 liegt in {a1, ... , a5}.
Die Konjunktion
(AI x → CI x) ∧ AIa2 ist somit genau dann wahr, wenn AI x → CI x wahr ist. Dies ist aber genau dann der Fall, wenn AI x falsch oder CI x wahr ist.
AI x ist falsch für a6, ... , a9, CI x ist wahr für a5, ... , a9, also ist die ODER-Verbindung wahr für x = a5, ... , a9, also gibt es in der Interpretation unseres Beispiels solche x, welche die Formel erfüllen (x kann z.B. mit a5 belegt werden): Die Formel φ ist in dieser Interpretation wahr.
Die Interpretation erfüllt die Formel, d.h. ist Modell für die Formel: I |= φ.
In einer andern Interpretation könnte dieselbe Formel auch nicht wahr sein.
Man kann sich nun sicher gut vorstellen, dass es nicht trivial ist herauszufinden, ob eine Formel in jeder möglichen Interpretation wahr ist. Dies war bei der Aussagenlogik mithilfe der Wahrheitstafeln relativ einfach und durchaus computer-programmierbar.
In der Prädikatenlogik gibt es für jede Formel jedoch überabzählbar unendlich viele Interpretationen.
Bild rechts: Illustration zum Beispiel im grauen Kasten
AI : "Frau"; CI : ">190cm"
("Frau"(x) → ">190cm(x)) ∧ "Frau"(a2) wird erfüllt für x = a5, ... , a9, was bedeutet, dass die Existenzbehauptung ∃x (("Frau"(x) → ">190cm(x)) ∧ "Frau"(a2)) zutrifft.
11. Modellrelation
Die Modellrelation sagt, wann ein Ausdruck bei einer Interpretation in eine wahre Aussage übergeht (siehe Beispiele oben). Vor allem das Beispiel im grauen Kasten oben rechts zeigt exemplarisch, wie die Modellbeziehung festgelegt wird. Es sei hier deshalb auf eine formale Definition verzichtet.
Aufgabe: Man erfinde eine Interpretation, die den Ausdruck ∀v1fv0v1≡v0 wahr macht.
Mögliches Modell: Grundbereich ℝ², f: (v; w) ↦ v. Es gilt ∀v(f(v ; w) = v).
Die Folgerungsbeziehung
Wann folgt ein Ausdruck φ aus einer Menge Φ von Ausdrücken?
Φ |= φ genau dann, wenn jedes Modell von Φ auch Modell von φ ist.
Beispiel: {Gruppenaxiome} |= zu jedem Gruppenelement existiert ein Linksinverses.
Allgemeingültig (|=φ) ist ein Ausdruck genau dann, wenn er bei allen Interpretationen gilt.
12. Axiome und Schlussregeln für den prädikatenlogischen Kalkül
Man hat eine mathematische Theorie, z.B. die Theorie der Gruppen.
Dass eine Aussage aus den Axiomen der Theorie folgt, ist durch einen Beweis zu zeigen.
Man habe eine Symbolmenge S und eine Menge
Φ von S-Sätzen. Sei Φ|= die Menge der S-Sätze, die aus Φ im Sinne der (semantischen) Folgerungsbeziehung oben folgen. Ein mathematischer Beweis für einen S-Satz φ muss zeigen, dass φ zu Φ|= gehört.
Die grosse Umkehrfrage lautet nun: Kann jeder Satz aus Φ|= via die Axiome aus Φ (syntaktisch) bewiesen werden?
Wie können wir elementare Schlussregeln aufspüren?
Wir versuchen, einen Katalog an Schlussregeln aufzustellen und einen Kalkül K zu erzeugen. Wir definieren dann, was "formal beweisbar" heisst. Damit sind wir dann wieder auf der syntaktischen Ebene.
Bemerkung: |
Der Kalkül garantiert die Korrektheit, d.h. was formal abgeleitet werden kann, garantiert auch die semantische Folgerungsbeziehung. Es gilt für den prädikatenlogischen Kalkül auch die Umkehrung: Gilt die semantische Folgerungsbeziehung, so kann gibt es auch eine entsprechende formale Ableitung.
Beispiel Gruppentheorie; Satz σ:
∀x ∃y y ο x = e, d.h. zu jedem x existiert ein Linksinverses y.
Mathematisch-semantischer Beweis:
1) ∀x ∃y x ο y = e (Gruppenaxiom 3)
2) ∀y ∃z y ο z = e (Gruppenaxiom 3)
3) y ο x = (y ο x) ο e (Gruppenaxiom 2)
4)
y ο x = (y ο x) ο (y ο z) (nach Schritt 2)
5)
y ο x = y ο (x ο (y ο z)) (Gruppenaxiom 1; Assoziativgesetz)
6)
y ο x = y ο ((x ο y) ο z) (Gruppenaxiom 1)
7)
y ο x = y ο (e ο z) (nach Schritt 1)
8)
y ο x = (y ο e) ο z (Gruppenaxiom 1)
9)
y ο x = y ο z (Gruppenaxiom 2)
10)
y ο x = e (nach Schritt 2)
Der mathematische Beweis entspricht nicht der Syntax des formalen Kalküls (Spalte rechts).
Die formale Ableitung verwendet hingegen die Syntax des Kalküls plus als Voraussetzung die 3 Gruppenaxiome φ1, φ2, φ3:
φ1: ∀x∀y∀z (x ο y) ο z = x ο (y ο z) (Assoziativität von ο)
φ2: ∀x x ο e = x (e ist rechtsneutral)
φ3: ∀x ∃y x ο y = e (Existenz eines Rechtsinversen zu jedem x)
Ebbinghaus (s. oben) gibt eine rein formale Ableitung von Satz σ in Bezug auf seinen Sequenzenkalkül.
Axiome
Axiome der Aussagenlogik:
A1: φ→ (ψ →φ): Abschwächungsregel
A2: (φ→ (ψ→ χ)) → ((φ→ψ) → (φ→χ)): Transitivität von →
A3: (¬ψ→ ¬φ) → (φ→ψ): Kontraposition
Axiome für die Quantoren:
A4:
∀x φ(x) → φ(σ), falls keine Variable von σ durch die Substitution in den Wirkungsbereich eines Quantors von φ gelangt.
A5:
∀x (φ→ψ) → (φ→∀x ψ), falls x nicht frei in φ.
Armin P. Barth fügt noch zwei Axiome für den Existenzquantor hinzu:
E1: φ(τ) → ∃x φ(x) (Existenzeinführung im Sukzedens)
E2: ∃x φ(x) → ¬∀x ¬φ(x)
Axiome für die Gleichheit:
A6: x = x: Reflexivität
A7: (x = y) → (y = x): Symmetrie
A8: (x = y) ∧ (y = z) → (x = z): Transitivität
A9: (x = y) → (Pi(..., x, ...) → Pi(..., y, ...))
A10: (x = y) → (fi(..., x, ...) → fi(..., y, ...))
Schlussregeln
Modus ponens:
φ
φ→ ψ
--------
ψ
Generalisierungsregel:
φ
--------
∀xφ
Quelle: Ernest Nagel, James R. Newman: Der Gödelsche Beweis, Oldenbourg Verlag, München 2001.
13. Einleitung
Eine mathematische Theorie entsteht durch ein Set von Axiomen zusammen mit dem Kalkül der Logik (z.B. der Prädikatenlogik 1. Stufe).
Die in den Axiomen vorkommenden Begriffe definieren sich implizit, d.h. einfach durch die via Axiome festgelegten Beziehungen. Man löst sich dabei von inhaltlichen Vorstellungen.
Ein rein formaler Beweis eines Satzes verwendet nun mechanisch-formal die Kalkülregeln zusammen mit den Aussagen der Axiome.
Der Regelsatz des Kalküls ist endlich.
Analogie zum Schachspiel:
Schachspiel
↔ Kalkül
Figuren und Felder ↔ Zeichen
zulässige Figurenstellungen ↔ Formeln ("wohlgeformte Zeichenketten")
Anfangsstellung ↔ Axiome
Folgestellungen ↔ Sätze, Theoreme
Spielregeln ↔ Ableitungsregeln
"Matt in 3 Zügen" ↔ eine metamathematische Aussage
Wir haben oben (Schluss von Pt. 6, grauer Kasten) gesehen, dass aus einem Widerspruch Beliebiges folgt, d.h. dass dann jede Formel ein Satz ist.
Dann gilt natürlich auch: Wenn nicht jede Formel ein Satz ist, dann ist der Kalkül widerspruchsfrei, d.h. es muss mindestens eine Formel geben, die nicht aus den Axiomen abgeleitet werden kann. (Denn wenn der Kalkül widersprüchlich wäre, wäre ja jede Formel ein Satz.)
Wir zeigen die Widerspruchsfreiheit der Aussagenlogik:
Sei t die Eigenschaft "tautologisch sein", d.h. allgemeingültig wahr sein (siehe die Wahrheitstabellen oben (Pt. 3). Die Axiome haben t und vererben t auch weiter. Jeder Satz besitzt somit t.
Wir suchen nun eine Formel, welche t nicht besitzt. Das ist z.B. p ∨ q. Denn wenn p und q falsch sind, ist auch p ∨ q falsch. p ∨ q ist somit kein Satz, aber eine Formel. Damit ist die Widerspruchsfreiheit der Aussagenlogik gezeigt.
Aussagen- und Prädikatenlogik als relativ einfache Kalküle sind vollständig, d.h. aus |- folgt |= und aus |= folgt |-.
Wir benötigen jedoch für die Mathematik viel komplexere Kalküle, namentlich solche, welche (z.B. via die Axiome der ZFC-Mengenlehre) die Arithmetik der natürlichen Zahlen enthalten. Und damit befasste sich Kurt Gödel.
Gödel zerstörte die Idee, dass ein hinreichend interessantes Gebiet der Mathematik (insbesondere die Arithmetik) durch ein vollständiges Axiomensystem charakterisiert werden kann. Das heisst: Es gibt wahre mathematische Sätze, die im System nicht abgeleitet werden können. Dies ändert sich auch nicht, wenn man immer neue Axiome hinzufügt.
Es gibt zudem auch keinen metamathematischen Beweis für die Widerspruchsfreiheit eines solchen Systems, ausser man benütze Umformungsregeln, die das System überschreiten und die wären dann auch wieder anzweifelbar, usw.
Idee Gödels zum Beweis seiner Sätze: Metamathematische Sätze ins System hineinspiegeln und dann eine Art Antinomie erzeugen. Dies geschieht mittels sogenannter Gödelzahlen (s. oben, Schluss von Pt. 5, grauer Kasten).
14. Gödelzahlen
Hier eine mögliche Zuordnung von Gödelzahlen zu einzelnen Zeichen (nach E.Nagel):
| Zeichen | Bedeutung | Gödelzahl |
| ¬ | 1 | |
| ∨ | 2 | |
| → | 3 | |
| ∃ | 4 | |
| = | 5 | |
| 0 | 6 | |
| s | Successor (Nachfolgezahl) | 7 |
| ( | 8 | |
| ) | 9 | |
| , | 10 | |
| x, y, z, ... | Zahlvariable | Primzahl > 10 |
| p, q, r, ... | Satzvariable | Primzahlquadrat > 10 |
| P, Q, R, ... | Prädikatsvariable | Primzahlkubik > 10 |
Weitere Junktoren und der Allquantor werden auf die in der Tabelle erwähnten zurückgeführt. Beispiel:
p ∧ q = ¬ (¬ p ∨ ¬ q).
1 ist definiert als s0, usw.
Beispiel einer Formel: (∃ x) (x = sy) wird folgendermassen gödelisiert:
| ( | ∃ | x | ) | ( | x | = | s | y | ) |
| 8 | 4 | 11 | 9 | 8 | 11 | 5 | 7 | 13 | 9 |
Diese Zahlen nehmen wir als die Exponenten der ersten 10 Primzahlen:
28 ⋅ 34 ⋅ 511 ⋅ 79 ⋅ 118 ⋅ 1311 ⋅ 175 ⋅ 197 ⋅ 2313 ⋅ 299 = : m
Das ist eine riesige Zahl in der Grössenordnung
1086.
So erhält auch jede Formel eine Gödelzahl.
Übung: Man bestimme die Gödelzahl von 1.
Lösung: 1 wird notiert als s0. Die Gödelzahl dazu ist
27 ⋅ 36 = 93'312.
Gödelisierung eines Beweisauschnitts:
(∃ x) (x = sy) Gödelzahl m
(∃ x) (x = s0) Gödelzahl n
Gödelzahl dieses Beweisauschnitts: 2m ⋅ 3n =: k
So erhält auch jede Formelfolge (d.h. jede formale Ableitung) eine eindeutige Gödelzahl.
Auf diese Weise wird der Kalkül vollständig arithmetisiert.
Achtung: Nicht jede Zahl ist eine Gödelzahl. 22 ⋅ 52 = 100 ist z.B. keine.
Welcher Formel entspricht die Gödelzahl 243'000'000?
243'000'000 = 26 ⋅ 35 ⋅ 56.
Die Abfolge 6, 5, 6 entspricht der Formel 0 = 0 (siehe Tabelle links).
Nun können alle metamathematischen Sätze über Eigenschaften des Kalküls im Kalkül selber abgebildet werden. Jeder metamathematische Satz wird eine arithmetische Formel (siehe Beispiele unten). Die logischen Abhängigkeiten zwischen den metamathematischen Sätzen werden zu numerischen Abhängigkeiten zwischen den arithmetischen Formeln.
Beispiel 1:
Der metamathematische Satz
"(p
∨ q) ist Vorderglied im Axiom (p
∨ q) → p"
wird so gespiegelt:
(p
∨ q) → p Gödelzahl a
(p
∨ q) Gödelzahl b
Gespiegelter Satz in der Arithmetik: b ist Teiler von a (das lässt sich arithmetisch formalisieren).
Beispiel 2:
"Die Formelfolge mit Gödelzahl x ist ein Beweis für die Formel mit Gödelzahl z."
Arithmetisch: Es gibt eine (sehr, sehr komplizierte) arithmetische Beziehung zwischen x und z, in Zeichen:
Dem(x, z).
*Dem" steht für "Demonstration", Herleitung.
Beispiel 3:
"Die Formelfolge mit Gödelzahl x ist kein formaler Beweis für die Formel mit Gödelzahl z."
Arithmetisch: ¬ Dem(x, z).
15. Grobe Ideen-Skizze des gödelschen Beweises
Diese "Gödelisierung" ist nur der Anfang des langen und mathematisch schwierigen Weges zum Beweis des ersten Unvollständigkeitssatzes, d.h. zur Konstruktion einer Aussage G der Zahlentheorie, die von sich selbst sagt: "Ich bin kein Theorem der Zahlentheorie, d.h. darin formal nicht herleitbar."
Näheres in eher beschreibender Form z.B. in Nagel: Der Gödelsche Beweis, Oldenbourg 2001.
Hier eine nochmals stark vereinfachte Skizze aus diesem bereits stark vereinfachenden Büchlein:
Betrachten wir nochmals die Formel (∃ x) (x = sy) mit Gödelzahl
m = 28 ⋅ 34 ⋅ 511 ⋅ 79 ⋅ 118 ⋅ 1311 ⋅ 175 ⋅ 197 ⋅ 2313 ⋅ 299 (s. Spalte oben links).
Die Gödelzahl der Variablen y ist 13. Wir ersetzen y durch m. Die Formel lautet dann
(∃ x) (x = sm).
Das bedeutet: "Es gibt eine Zahl x, die successor (unmittelbarer Nachfolger) von m ist.
Sei r die Gödelzahl von (∃ x) (x = sm) oder (∃ x) (x = sss...s0). (s tritt dabei m+1-mal auf.)
r = 28 ⋅ 34 ⋅ 511 ⋅ 79 ⋅ 118 ⋅ 1311 ⋅ 175 ⋅ 197 ⋅ 237⋅ 297⋅ 317⋅ ... p9 ,wobei p die (m+10)te Primzahl ist.
Nun vergleichen wir die Gödelzahlen m und r.
m enthält einen Primfaktor in 13. Potenz, nämlich
2313. r enthält alle Primfaktoren von m und noch viele weitere, aber keiner ist in die 13. Potenz erhoben! Man erhält also r aus m, indem man 2313 durch andere Primfaktoren in von 13 verschiedenen Potenzen ersetzt. r ist somit eine ganz bestimmte arithmetische Funktion von m und von 13.
Wir schreiben: r = sub(m, 13, m). Das ist die Gödelzahl der Formel, die man aus der Formel mit Gödelzahl m erhält, wenn y, also die Variable mit Gödelzahl 13,
durch m substituiert wird.
sub(y, 13, y) bedeutet die Gödelzahl der Formel, die man aus der Formel mit Gödelzahl y erhält, indem für die Variable mit Gödelzahl 13, also für y, das Zahlzeichen für y eingesetzt wird.
y ↦ sub(y, 13, y) ist eine arithmetische Zuordnung (Gödelzahl ↦ Gödelzahl).
Was bedeutet etwa sub(243'000'000, 13, 243'000'000)? Es ist die Gödelzahl der Formel mit Gödelzahl 243'000'000, also der Formel 0 = 0, in welcher die Variable mit Gödelzahl 13, also die Variable y, durch das Zahlzeichen 243'000'000 ersetzt wird. Da in dieser Formel y nicht vorkommt, entsteht nach dieser "leeren Substitution" dieselbe Formel, also erneut 0 = 0 mit Gödelzahl 243'000'000. Es ist somit
sub(243'000'000, 13, 243'000'000) = 243'000'000.
Noch ein Beispiel:
Wir betrachten die Formel
y = 0.
Ihre Gödelnummer ist
213⋅35⋅56 = 31'104'000'000.
Wir betrachten sub(31'104'000'000, 13 , 31'104'000'000).
Das ist die Gödelnummer der (inhaltlich falschen) Formel
31'104'000'000 = 0, d.h. der Formel sss...s0 = 0,
wobei 31'104'000'000 Buchstaben s aufeinanderfolgen.
Die Gödelnummer sub(31'104'000'000, 13 , 31'104'000'000)
ist dann 27⋅37⋅...⋅p6⋅q5⋅r6,
wobei p die (31'104'000'000+2)te, q die (31'104'000'000+3)te und r die (31'104'000'000+4)te Primzahl ist.
Die Formel ¬ Dem(x, z) wurde oben eingeführt. Sie lautet metamathematisch: "Die Formelfolge mit Gödelzahl x ist kein Beweis für die Formel z".
Nun setzen wir: (∀x) ¬ Dem(x, z). (Der Allquantor kann mithilfe des Existenzquantors ∃ ausgedrückt werden.)
Dies besagt: "Für jedes x gilt, dass die Formelfolge mit Gödelzahl x kein Beweis für die Formel mit Gödelzahl z ist", was bedeutet: "Die Formel mit Gödelzahl z ist nicht beweisbar".
Gödel zeigte nun, dass ein Spezialfall dieser Formel (∀x) ¬ Dem(x, z) formal nicht herleitbar ist; dieser Spezialfall würde dann metamathematisch die Wahrheit ausdrücken: "Ich bin formal nicht herleitbar".
Wie entsteht nun dieser Spezialfall?
Wir betrachten (∀x) ¬ Dem(x, sub(y, 13, y)).
Metamathematisch: "Die Formel mit der Gödelzahl
sub(y, 13, y) ist formal nicht herleitbar."
Diese Formel (∀x) ¬ Dem(x, sub(y, 13, y)) habe die Gödelzahl n.
Nun bilden wir (∀x) ¬ Dem(x, sub(n, 13, n)) =: G ("Gödel"). Dies ist der gesuchte Spezialfall. Die Gödelzahl von G ist per Konstruktion sub(n, 13, n).
G heisst metamathematisch: "Die Formel mit der Gödelzahl sub(n, 13, n) -und das ist eben gerade G selber!- ist formal nicht herleitbar." G sagt also gewissermassen: "Ich bin formal nicht herleitbar."
Das bedeutet nun noch nicht, dass G tatsächlich formal nicht herleitbar wäre (G könnte ja "lügen"). Dass G tatsächlich formal nicht herleitbar ist, muss noch gezeigt werden. (It's not over till it's over!).
Falls der Kalkül korrekt ist, ist jede formal hergeleitete Aussage wahr. Könnte G formal hergeleitet werden, wäre die Aussage "Ich kann nicht hergeleitet werden" falsch. Das kann in einem korrekten Kalkül nicht sein. Also kann G nicht hergeleitet werden, und G ist wahr. ¬G ist als falsche Aussage ebenfalls nicht herleitbar. Wir haben eine wahre, aber formal unentscheidbare Aussage gefunden.
Das wäre die semantische Fassung von Gödels Unvollständigkeitssatz.
Gödel zeigte jedoch mehr: eine syntaktische Fassung des Satzes. Er zeigte, dass genau dann, wenn G formal herleitbar wäre, es auch ¬G wäre. (Er benötigte dazu eine Voraussetzung an den Kalkül, der als ω-widerspruchsfrei bezeichnet wird.)
Vorausgesetzt, der Kalkül sei widerspruchsfrei, ist es nicht möglich, dass sowohl G wie auch ¬G herleitbar sind, also ist unter dieser Voraussetzung G formal nicht herleitbar (ebensowenig ¬G). G ist formal unentscheidbar.
G ist metamathematisch wahr, d.h. es gibt eine wahre arithmetische Formel, die formal nicht herleitbar ist.
16. Eine Bemerkung
Hilberts Programm, die Mathematik auf eine endgültig gesicherte, unveränderliche formale Grundlage zu stellen ist aufgrund des Gödelschen Unvollständigkeitssatzes gescheitert. Für Hilbert war dies ein nicht leicht hinzunehmender Schlag, den er akzeptieren musste.
Ist Gödels Resultat aber nicht im Gegenteil etwas Positives? Es zeigt doch die "ewige" Offenheit der Mathematik für Neues. Kein Formalismus (der die Zahlentheorie umfasst) ist je vollständig. Die Mathematik wird sich so immer wieder entwickeln und verändern können - das letzte Wort ist nie gesprochen! - Wäre nicht die Erfüllung von Hilberts Traum einer endgültigen, unveränderlichen Formalisierung dagegen eher deprimierend gewesen?
Im Sinne Hermann Weyls könnte man sagen: Es geht nie um zeitlose Letztbegründungen! Besser als ein Trugbild der Zeitlosigkeit ist ein Konzept von "Fortsetzbarkeit". Und genau dies wird durch Gödels Sätze unterstrichen.
Und noch eine Bemerkung zur Poesie des nie Vollendbaren:
Un poème n'est jamais fini, seulement abandonné. (Paul Valéry)
Solomon Feferman zu Gödels Unvollständigkeitssätzen und Gedanken dazu.
(Gödel on minds and machines.)
Torkel Franzén: The Popular Impact of Goedel's Incompleteness Theorem
Warnung vor der Versuchung, die Unvollständigkeitssätze über die Mathematik hinaus zu strapazieren. Solche Grenzüberschreitungen wurden früher auch mit der Heisenbergschen Unschärferelation begangen.
Was wäre gewonnen, wenn die ZFC-Mengentheorie entgegen Gödels Satz ihre eigene Widerspruchsfreiheit beweisen könnte? - Nichts, denn wäre sie trotzdem widersprüchlich, könnte jede Aussage, also auch die Widerspruchsfreiheit, bewiesen werden. Wir wären so klug als wie zuvor.