Gegeben sei eine Daten-Zeitreihe f(i), z.B. wie folgt:
(1.55; 2.86; 2.19; 1.9; 1.75; 2.28; 2.52; 1.46; 1.48; 1.69; 2.98; 1.4; 1.93).
Oftmals möchte man -z.B. um Saisonausschläge auszublenden, damit saisonunabhängige Trends sichtbar werden- solche Daten glätten.
Eine Möglichkeit besteht im Erzeugen einer neuen Datenfolge b(i) mit
b(i) = [f(i-1) + f(i) + f(i+1)] / 3.
Man bildet also Mittelwerte dreier benachbarter f-Werte. (Es können statt "Dreierfenster" auch andere Fenster, z.B. Fünferfenster, verwendet werden.) Vorzugsweise wählt man eine ungerade Fenstergrösse (in unserem Beispiel 3), damit man eine Fenstermitte vorfindet.
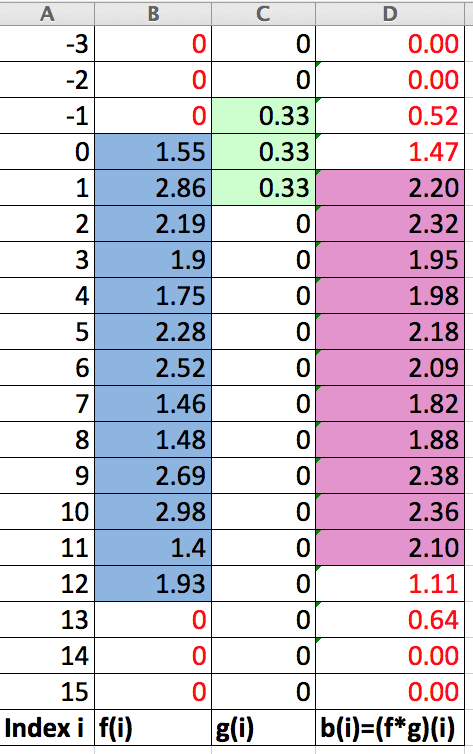
Die Tabelle rechts zeigt links (blau) die f-Reihe (Originaldaten) f(0) bis f(12). Für die übrigen Indices i wird f(i) = 0 gesetzt. So entsteht eine diskrete Funktion f, die auf der Menge ℤ der ganzen Zahlen definiert ist.
Man kann sich nun vorstellen, dass ein Fenster, das genau drei benachbarte Daten zeigt, über die f-Werte fährt (grün in der Tabelle). Dabei wird stets der Mittelwert der gezeigten Fensterzahlen gebildet.
So entsteht die geglättete, violett dargestellte Folge (b(i)).
Beispiel einer Berechnung: b(5) = (1/3)⋅f(6)+(1/3)⋅f(5)+(1/3)⋅f(4)=2.18.
Dieser Wert entsteht gewissermassen als Skalarprodukt
<f(6), f(5), f(4)>⋅<1/3, 1/3, 1/3>.
Noch eine interessante Bemerkung:
Die Summe der f-Werte (1.55 + ... + 1.93) ist hier gleich der Summe der b-Werte
(0.52 + 1.47 + 2.20 + ... + 2.10 + 1.11 + 0.64).
Dies ist hier deshalb der Fall, weil die Summe der g-Werte (der Gewichte) gleich 1 ist.
Allgemein gilt:
∑b(i) = ∑f(i) ⋅ ∑g(i).
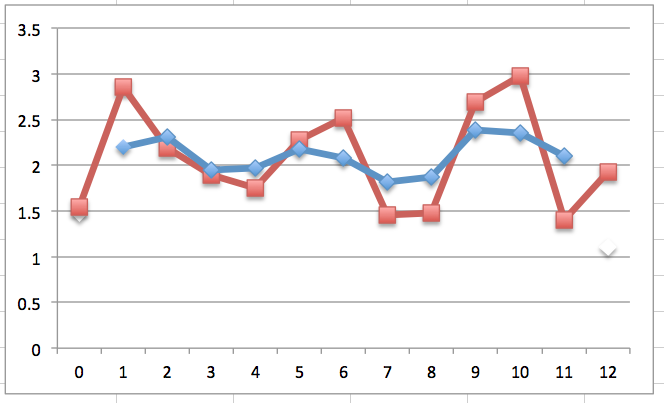
Bild links:
rot: ursprüngliche f-Datenreihe
blau: geglättete b(i)-Reihe.
Man sieht: Die wirtschaftlich verwendbaren b(i)-Werte beginnen bei b(1) und enden bei b(11), während die f-Daten von f(0) bis f(12) reichen.
Definition der Faltung (f∗g) einer diskreten Funktion f mit einer diskreten Funktion g:
Obiger Vorgang des Glättens mittels gleitender Durchschnitte kann mathematisch als Faltung (f∗g) der Funktion f mit der Funktion g beschrieben werden, wenn wir g wie im Falle unseres Dreierfensters wie folgt definieren:
g(-1)=g(0)=g(1) = 1/3; g(i)=0 sonst. Der Definitionsbereich von g sei die Menge ℤ der ganzen Zahlen.
g ist dann eine Rechteckfunktion, die nur an 3 Stellen, nämlich für die Argumente -1, 0 und 1, den Wert 1/3 annimmt und für alle übrigen Argumente den Wert 0 liefert. g ist unser Dreierfenster.
Die Definition einer Faltung f∗g zweier diskreter Funktionen f und g (mit gleichem Definitionsbereich aus ℤ) liefert nun für unsere Wahl von g gerade die Dreier-Mittelwerte:
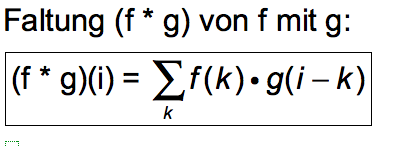

Beispiel für eine gleitende Mittelung von Umsatzdaten über ein Quartal:
Will man etwa quartalsweise mitteln, wählt man oft ein Fünferfenster und gewichtet den ersten und den letzten Fensterwert nur halb so stark wie die drei mittleren Werte.
g sieht dann wie folgt aus:
g(-2)=g(2)=1/8; g(-1)=g(0)=g(1)=1/4. g(i)=0 sonst.
Mit den Daten aus der Tabelle ganz oben sähe dann b(2) so aus:
b(2) =(1/8)⋅f(4)+(1/4)⋅f(3)+(1/4)⋅f(2)+(1/4)⋅f(1)+(1/8)⋅f(0)=2.15.
Asymmetrischer Filter und Faltungsformel:
Sei ein asymmetrischer Filter wie folgt definiert:
b(i) = (1/8)⋅f(i-1)+(3/8)⋅f(i)+(4/8)⋅f(i+1).
Beispiel: b(2) = (1/8)⋅f(1) + (3/8)⋅f(2) + (4/8)⋅f(3).
(Es kann z.B. sinnvoll sein, weiter zurück liegende Daten weniger stark zu gewichten als näher liegende.)
g muss dann, wie die nebenstehende Rechnung zeigt, wie folgt definiert werden:
g(-1) = 4/8, g(0) = 3/8, g(1) = 1/8.
Das mag auf den ersten Blick etwas überraschen: Der g-Filter erscheint gewissermassen horizontal gespiegelt.
Beispiel:
b(2) = ∑f(k)⋅g(2-k) = f(3)⋅g(-1) + f(2)⋅g(0) + f(1)g(1)
= f(3)⋅(4/8) + f(2)⋅(3/8) + f(1)⋅(1/8)Warum muss g gewissermassen horizontal gespiegelt definiert werden?
Wir machen uns mithilfe einer Grafik klar, wie die Faltungsformel wirklich "zählt".
Hier nochmals die Faltungsformel:
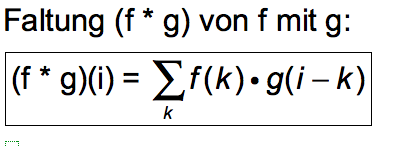
Zwei mögliche Arten zu zählen:
Die Mittelung der f-Daten mithilfe des g-Filters kann auf zwei Arten geschehen:
1)
Ich kann an einer Stelle i ein Dreierfenster über die Daten legen und
den linken Wert mit 1/8, den mittleren mit 3/8 und den rechten mit 4/8 gewichten. Das ergibt dann meinen geglätteten b(i)-Wert.
Aber auf diese Weise zählt die Faltungsformel eben gerade nicht!
2)
So zählt die Faltungsformel:
Ich wähle wieder eine Stelle i in der Folge der f-Daten (Bildserie rechts: roter Kreis).
Nun verschiebe ich das Schablonenfenster g um k, d.h. ich bilde die verschobene Funktion g(x-k). Die Fenstermitte steht nun an der Stelle k (grünes Fähnchen in der Bildserie rechts).
Nun werte ich dieses verschobene Fenster an der fest gewählten Stelle i aus (an der Stelle unterhalb des roten Kreises in der Bildserie rechts), d.h. ich bilde g(i-k).
Diesen Wert multipliziere ich mit f(k).
Dann lasse ich k weiter laufen. k läuft so durch ganz ℤ hindurch.
In unserem Beispiel mit dem Dreierfenster sind nach 3 Schritten alle g(k) ≠ 0 ausgewertet und mit den f-Werten verknüpft.
Resultat: Ich habe ebenfalls von f(i-1), f(i) und f(i+1) das gewichtete Mittel bestimmt.
f(i-1) wurde jedoch mit dem rechten Fensterwert, f(i) mit dem mittleren und f(i+1) mit dem linken Fensterwert von g verknüpft.
Somit muss ich die g-Schablone horizontal gespiegelt definieren.
Die Bildfolge rechts illustriert diesen Vorgang.
Für jedes fest gewählte i entsteht so das gewichtete Mittel (ein Skalarprodukt); das ist der i-te Funktionswert der Faltung, also (f*g)(i).
Zusammenfassung: g wandert über die fest gewählte Stelle i und wird dort jeweils ausgewertet: g(i - k). Dieser Wert wird multipliziert mit dem f-Wert beim Fähnchen, also mit f(k). Summiert über alle k ergibt sich das gewichtete Mittel (Skalarprodukt).
Dieser Wert ist (f∗g)(i).
Da der rechte Fensterrand zuerst verwertet wird, muss der g-Filter in umgekehrter Zeitrichtung notiert werden.
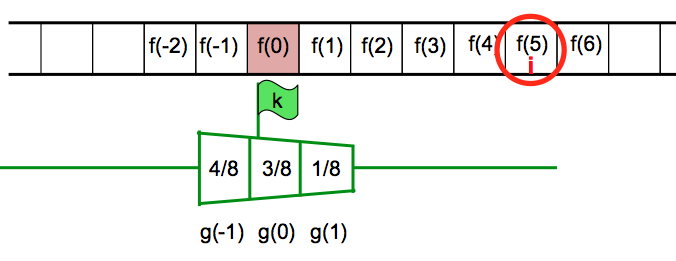
Datenreihe f und Filterfunktion g. Rot: Gewählte Stelle i. Das grüne Fähnchen gibt die Position k des Filterfensters (Fenstermitte) an.
Im Bild oben ist k = 0, i = 5.
g ist wie im Bild gezeigt definiert: g(-1) = 4/8, g(0)=3/8, g(1)=1/8, für die übrigen Argumente ist g(k) = 0.
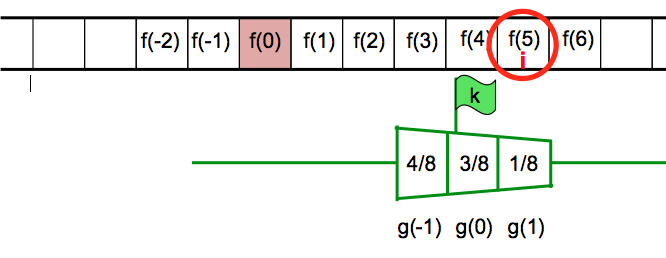
g wurde um 4 Einheiten nach rechts verschoben, wird also zu g(x-4). Die Auswertung dieser verschobenen Funktion an der Stelle i ist g(i-4) = g(5-4) = g(1) = 1/8 (Wert unter dem roten Kreis). Diesen Wert multiplizieren wir mit dem f-Wert beim Fähnchen, also mit f(4).
Es entsteht f(4)⋅(1/8).
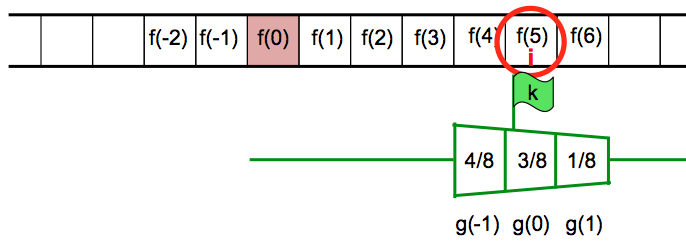
g wird nun um 5 Einheiten nach rechts verschoben und bei i ausgewertet: g(i-5) = g(0) = 3/8 (Wert unter dem roten Kreis). Dieser Wert wird multipliziert mit dem f-Wert beim Fähnchen, also mit f(5).
Es entsteht
f(5)⋅(3/8).
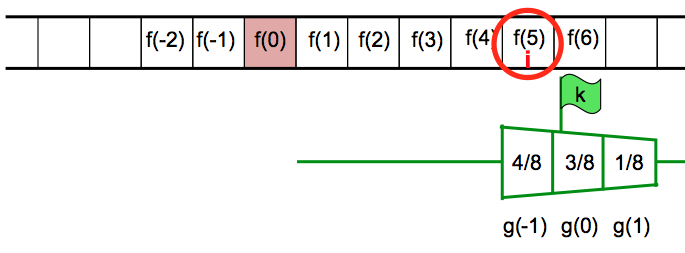
Nochmals eine Verschiebung. Es entsteht f(6)⋅(4/8).
Bei weiteren Verschiebungen entsteht nichts Neues mehr, da die Auswertung von g bei i stets 0 ergibt. Wir haben 3 Summanden: f(4)⋅(1/8) + f(5)⋅(3/8) + f(6)⋅(4/8).
In der Wirtschaft hat man es oft mit diskreten Zeitreihenfunktionen zu tun; in der Technik kommen eher stetige Funktionen zur Anwendung. Aus der Summe in der Definition der Faltung wird dann ein Integral:
![]()
Faltung stetig:
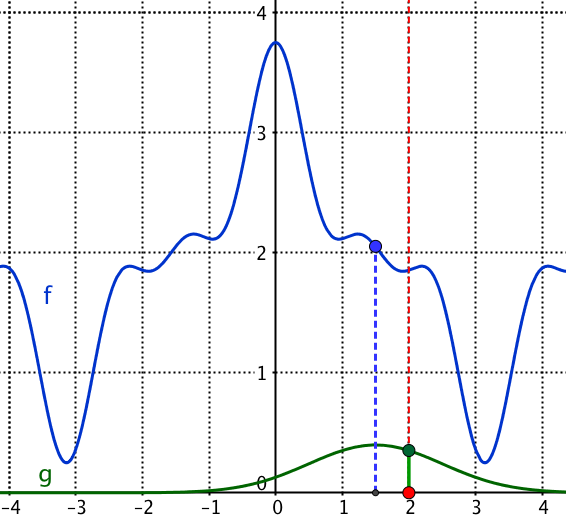
Die Gewichtungsfunktion g (auch Faltungskern genannt) wurde hier um τ = 1.5 nach rechts verschoben und wird zu g(x-τ), also hier zu g(x-1.5).
Als feste x-Stelle wurde im Bild oben
X = 2 gewählt.
Es wird dann g(X - τ), also hier g(2 - 1.5) = g(0.5) berechnet (kleine senkrechte grüne Linie im Bild oben).
Dieser Wert wird mit f(τ), also hier mit f(1.5) multipliziert (senkrechte, gestrichelte, blaue Linie im Bild).
Nun wird
τ verändert, d.h. g wird über den ganzen Definitionsbereich hinweg "durchgescannt", und es wird über alle entstehenden Produkte
f(τ )⋅g(X- τ)⋅dτ integriert.
Für X = 2 entsteht so ein Zahlenwert: der Wert der Faltung an der Stelle X .
Wie kann man sich den Übergang vom diskreten zum stetigen Fall vorstellen?
f und g seien nun Funktionen auf ℝ. Wir können uns als Übergang vom Diskreten zum Stetigen vorstellen, dass die Funktionen ganz fein gerasterte Treppenfunktionen sind. Die Einzelschritte haben dann nicht mehr Schrittlänge 1, sondern Schrittlänge Δτ.
Wir legen wieder eine fixe Stelle X fest. Wir markieren sie wieder, wie oben, rot.
g verschieben wir sukzessive mit wachsenden Werten τ
nach rechts und werten diese verschobene Funktion bei X aus. Es entsteht g(X - τ).
τ schreitet nun nicht mehr in Einerschritten, sondern in Schritten von Δτ voran.
Wir bilden für jedes τ das Produkt f(τ
)⋅g(X- τ)⋅Δτ.
Wir scannen also gewissermassen mittels aller möglicher Werte von τ den ganzen Definitionsbereich ab und summieren dabei alle Werte f(τ )⋅g(X - τ)⋅Δτ auf.
Diese Summe, ∑ f(τ )⋅g(X- τ)⋅Δτ, die nach einem solchen Scan entsteht, ist der Wert der Faltung an der Stelle X.
f(X) wurde durch diesen Vorgang ersetzt durch das mit g gewichtete Mittel.
So verfahren wir mit allen möglichen Wahlen von X.
Wird Δτ immer kleiner, strebt die Summe gegen ein Integral und aus Δτ wird dτ.
Darstellung der Faltung (f ∗ g) in Geogebra
Funktion f definieren.
Filterfunktion g definieren.
Regler für die zu wählenden X-Stellen erzeugen.
Y: = ∫ f(τ )⋅g(X - τ)⋅dτ.
(In Geogebra muss statt der Integrationsvariablen τ die Variable x gewählt werden. Man beachte: Gross X bedeutet hier eine feste x-Stelle, klein x ist die Funktionsvariable.)
Es entsteht der Punkt R(X / Y).
Spur für R einschalten. Mit Regler X variieren: R wandert und es entsteht der Graph der Faltungsfunktion. Allenfalls Animation einstellen.
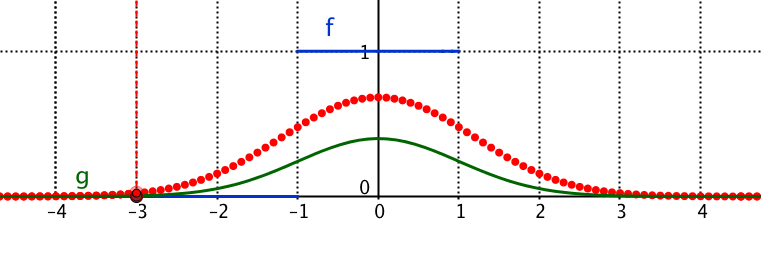
Faltung eines Rechteckimpulses (blau) mit einer auf Fläche 1 normierten Gausskurve g(x) = Exp[-x²/2] / 2.51 (grün).
Resultat rot.
Für die Intergration (s. Geogebra-Anleitung links) können die Integrationsgrenzen -1 und 1 gewählt werden, da f ausserhalb verschwindet.
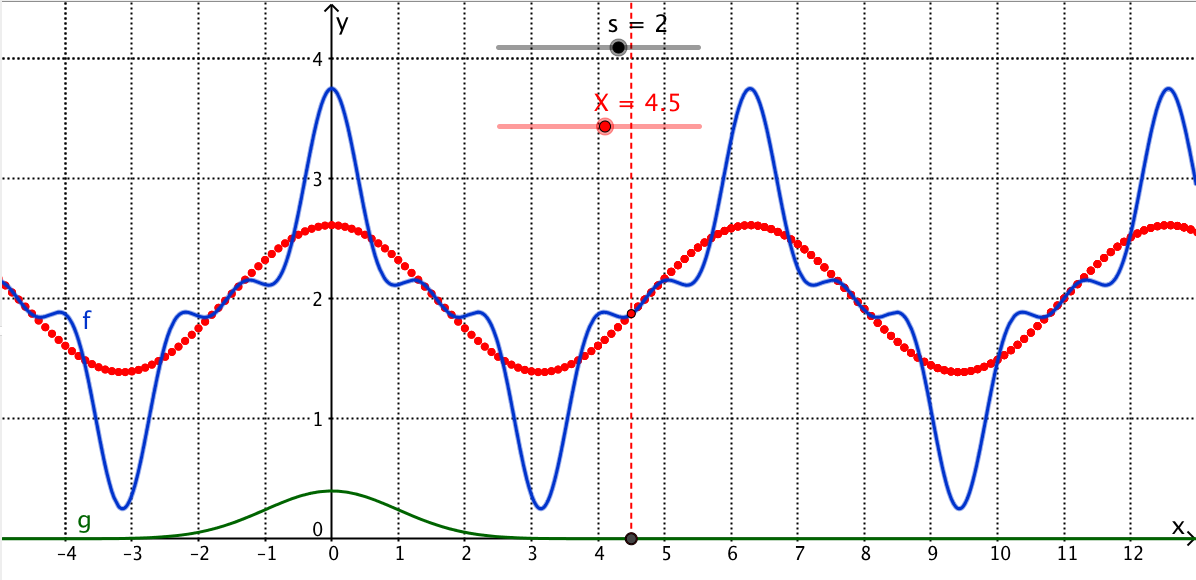
Faltung von f(x) = 2 + cos(x) + 0.5 cos(3x) + 0.25 cos(5x) (blau) mit der normierten Gaussfunktion g(x) = Exp[-x²/2] / 2.51 (grün). (Standardabweichung 2; schwarzer Regler oben.)
Resultat rot. Die Mittelung bzw. Glättung ist sehr schön sichtbar.
Für die Integration (s. Geogebra-Anleitung oben) genügen hier Integrationsgrenzen -20 und 20 (oder auch weniger), da die Gaussfunktion ausserhalb praktisch verschwindet.
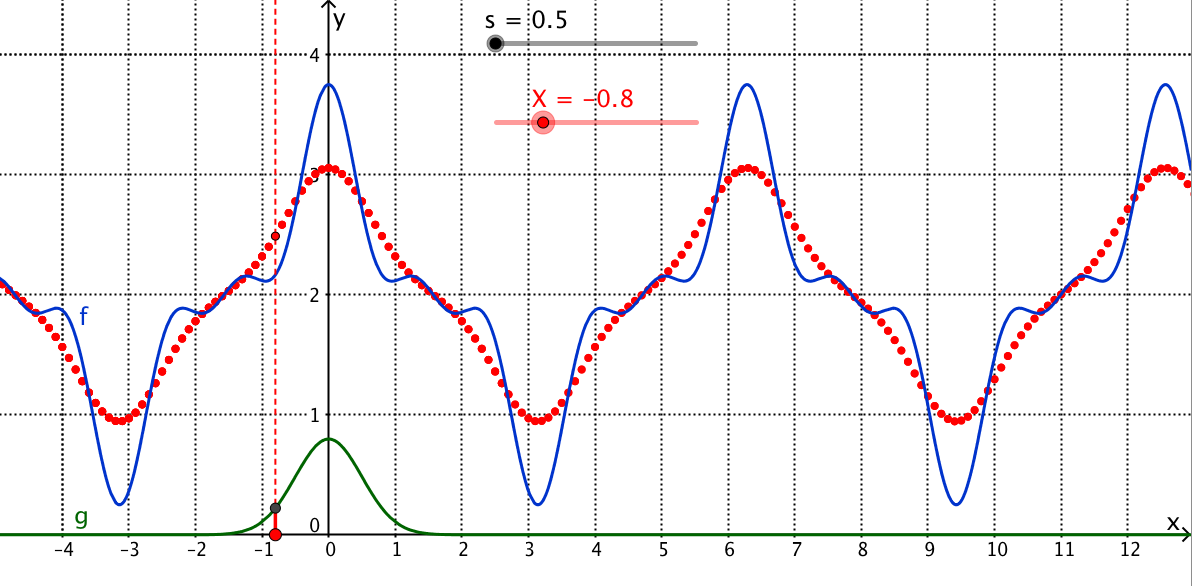
Faltung derselben Funktion f mit einer normierten Gaussfunktion mit schmalerer Standardabweichung (s = 0.5):
g(x) = Exp[-x²/0.5] / 1.25 (grün).
Resultat rot. Die Glättung wird weniger ausgeprägt.
Multiplikationsgesetz:
Es gilt (analog wie es ganz oben im diskreten Fall illustriert wurde):
∫(f∗g)(x)dx = ∫f(x)dx ⋅ ∫g(x)dx.
Ist g wie in den Beispielen oben normiert, d.h. ∫g(x)dx = 1, ist der Flächeninhalt unter der Faltungsfunktion gleich dem Flächeninhalt von f.
Faltung eines Rechteckimpulses mit einem Rechteckimpuls
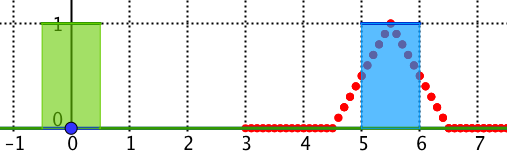
blau: Rechteckimpuls f: Für 5 ≤ x ≤ 6 ist f(x) = 1, sonst 0.
grün: Faltungskern g: Für -0.5 ≤ x ≤ 0.5 ist g(x) = 1, sonst 0.
rot gepunktet: die Faltung f ∗ g.
Es genügt, im Geogebra-Modell die Integrationsgrenzen zwischen τ = 5 und τ = 6 zu wählen. Ausserhalb davon ist f(τ) ohnehin 0. Genau für 4.5 ≤ X ≤ 6.5 ergibt auch g(X - τ) Werte ≠ 0: Die Überlappung der τ-verschobenen grünen Kernfunktion mit der blauen Funktion f beginnt bei τ = 4.5 und endet bei τ = 6.5.
Die Faltung ist eine Dreiecksfunktion.
Noch ein Beispiel
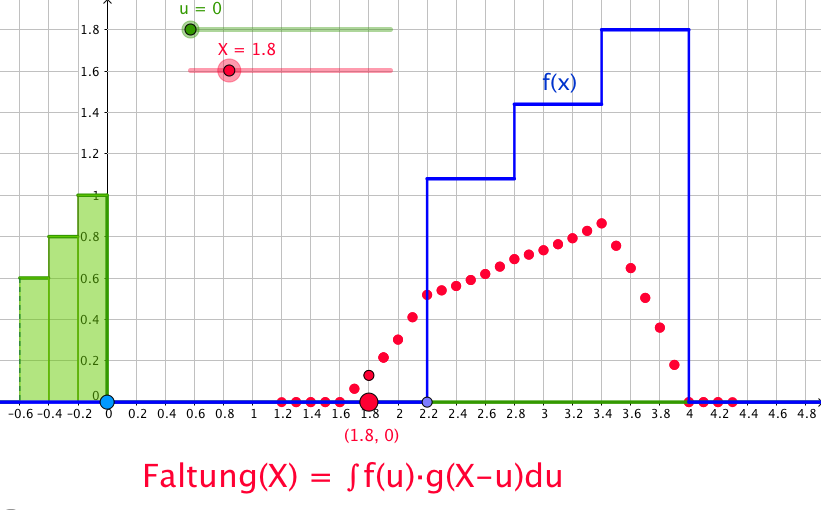
Das Modell reagiert ziemlich langsam (Rechenaufwand!). Es ist also beim Verschieben von X eine gewisse Geduld erforderlich.
Faltung der blauen Treppenfunktion f(x) mit der grünen Kernfunktion g(x).
g(x) wird sichtbar, wenn der Regler u auf 0 gestellt wird.
(Die Treppenintervalle seien links offen und rechts geschlossen.)
Sei F die Faltungsfunktion F: = (f ∗ g). Mit dem Regler X stellen wir die Stelle X ein, für die F(X) berechnet werden soll. (Bild oben: X = 1.8.)
g(x) wird nun mit dem Regler u nach rechts verschoben, d.h. wird zu g(x – u). Sobald diese Funktion einen Wert ≠ 0 ergibt, wird im dynamischen Geogebra-Modell eine grün gestrichelte Linie sichtbar, die den Funktionswert anzeigt.
Sobald die blaue Funktion einen Wert f(u) ≠ 0 ergibt, wird im dynamischen Geogebra-Modell eine blau gestrichelte Linie mit dem Funktionswert f(u) angezeigt. Dies ist dann der Fall, wenn u in den Bereich zwischen 2.2 und 4 gelangt.
Da für die Faltung f(u)⋅ g(X – u) du gebildet wird, entstehen Beiträge an die Faltung genau dann, wenn sowohl die grün-gestrichelte als auch die blau-gestrichelte Strecke aufleuchten.
Wir wählen also einen X-Wert. Dann scannen wir mittels des Reglers u die Kernfunktion durchs Bild und können beobachten, wie für eine Stelle X diese Faltungsbeiträge entstehen. Die Schrittweite fürs Durchscannen von g wurde als 0.1 gewählt. Solange beide gestrichelten Linien aufleuchten, entstehen Faltungsbeiträge für die Stelle X.
Verschiebt man den Regler X, wird die Faltungsfunktion gezeichnet (Animation starten; am besten u auf 0 stellen). Achtung: Geduld erforderlich, das Programm arbeitet langsam!
Stellt man z.B. X auf 1.8 (kleiner Faltungswert), sieht man, dass beim Verändern von u nur über einen sehr kleinen Bereich beide gestrichelten Linien aufleuchten, nämlich nur für u zwischen 2.2 und 2.4. Das gibt wenig Faltungsertrag.
Noch enger wird der zählende u-Bereich für X = 1.65. Es entstehen nur Faltungsbeiträge zwischen den u-Werten 2.2 und 2.25.
Für X = 3.4 ist hingegen der zählende u-Bereich gross. Er liegt zwischen den u-Werten 3.4 und 4: Es entsteht ein grosser Faltungswert. Auch für X = 2.8 ist der u-Bereich, der beide gestrichelten Linien zeigt gross, er liegt zwischen 1.8 und 3.4. Dort ist jedoch die Funktion f(x) noch kleiner als im Bereich 3.4 bis 4, weshalb der Faltungswert noch nicht seinen Maximalwert erreicht.
Man sieht, dass die Faltung mit g die Treppe f „erodieren“ lässt: Die scharfen Ecken werden „stumpfer“.
Wieder gilt der Multiplikationssatz: Flächeninhalt unter g mal Flächeninhalt unter f gleich Flächeninhalt unter der Faltungskurve.
Faltung einer einseitigen Exponentialfunktion (x > 0) mit einer Gaussfunktion:
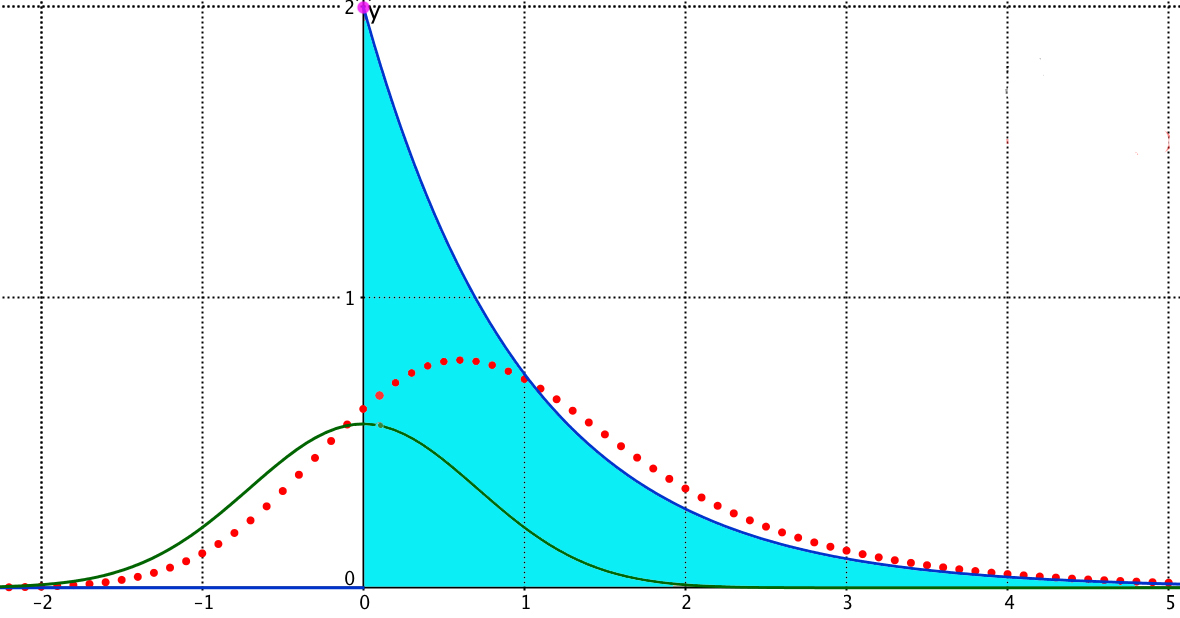
blau: einseitige Exponentialfunktion f
grün: Gaussfunktion g
rot gepunktet: Faltung f ∗ g
Nach Tilman Butz: Fouriertransformation für Fussgänger, 7. Auflage, Vieweg+Teubner, Wiesbaden, 2011, kann man sich ausgehend von der Spitze (0 / 2) des blau eingefärbten Berges - gebildet durch die Exponentialfunktion und die Steilwand (y-Achse) - eine Art "Erosion" vorstellen, die gleichwertig nach links und nach rechts stattfindet (die Gausskurve steuert diese Erosion). Die Spitze erodiert und es entsteht die rot gepunktet markierte Geröllhalde.