Die Linie - ein mathematisch-kultureller Rundgang

Spiralen

Die logarithmische Spirale

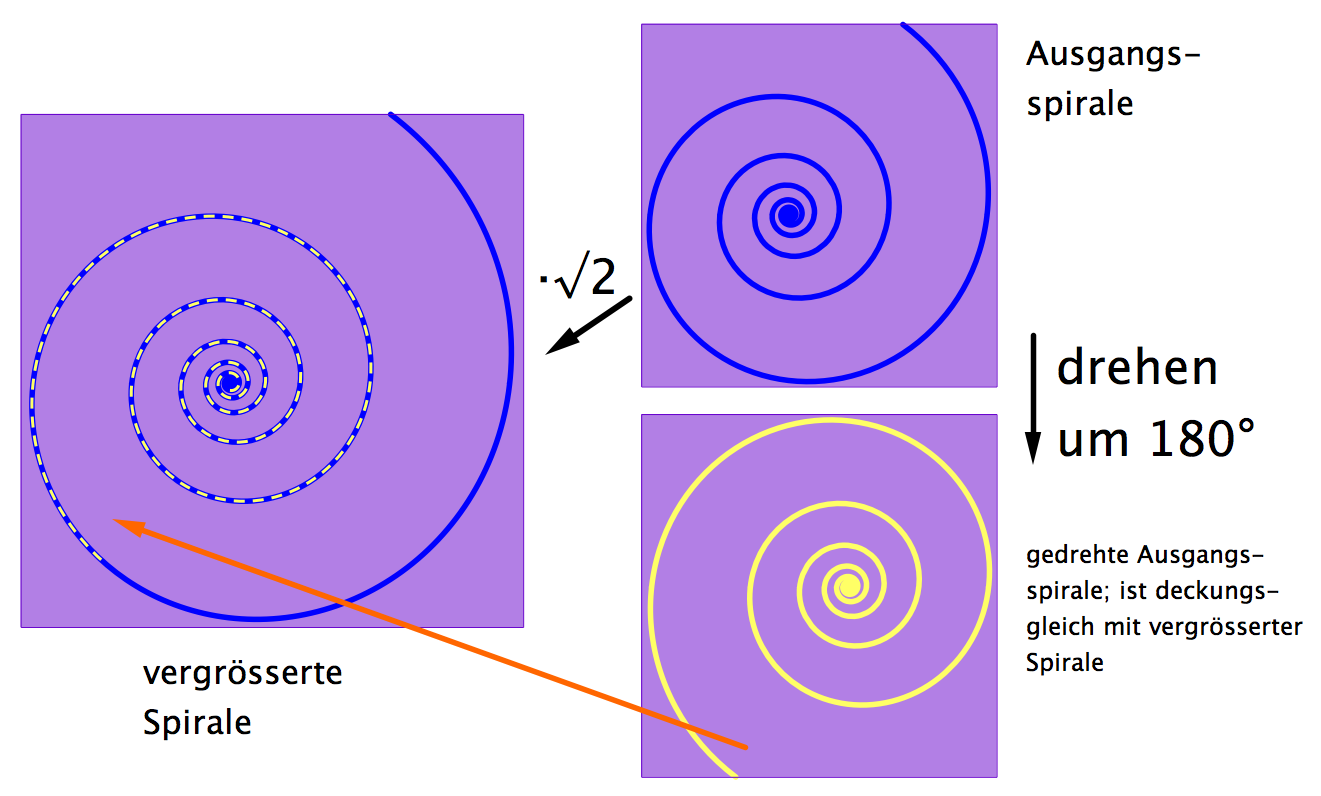
Die blaue Spirale startet mit Radius 1 auf der x-Achse. Der Radius zoomt sich pro 30°-Drehung kontinuierlich mit Faktor q auf. Nach einer Umdrehung hat der Radius die Grösse 2, nach einer weiteren Umdrehung die Grösse 4. Eine Umdrehung entspricht einem Oktavsprung bzw. einer Frequenzverdoppelung.

Es ist q¹² = 2 => q = 2^1/12 = 1.059463094...

Hat der Ton a' (Kammerton) die Frequenz 440 Hz, so sind die Frequenzen der folgenden Halbtöne gegeben durch 440*q, 440*q², 440*q³ , usw.

Die Spirale kann vom Startpunkt aus auch nach rückwärts weitergeführt werden (gestrichelte Linie). Dem entspricht ein Weiterschreiten zu tieferen Tönen. Pro Volldrehung halbiert sich der Radius der Spirale. Die Spirale erreicht den Nullpunkt nie.

Der hier gezeigte Anstieg der Frequenzen entspricht der gleichstufigen Stimmung. Die Oktave wird in 12 gleiche Halbtonschritte eingeteilt, wodurch die Intervalle auf einem Tasteninstrument bei jeder Transponierung gleich bleiben. Johann Sebastian Bachs "Wohltemperiertes Klavier" ist eine Reverenz an "wohltemperierte" Stimmungen (wenngleich es sich dabei noch nicht um die heutige gleichstufige Stimmung -basierend auf der zwölften Wurzel aus 2- handelte).

Föhrenzapfen. Die Schuppen sind spiralförmig angeordnet. Man erkennt zwei Sorten von Spiralformen (rot bzw. grün markiert). Von den roten "Spiralen" besitzt der Zapfen 8, von den grünen 13.

8 und 13 sind aufeinanderfolgende Fibonacci-Zahlen. Die Fibonacci-Folge ist folgende Zahlfolge:

0   1   1   2   3   5   8   13   21   34   55   ...

Jede Zahl der Folge ist jeweils die Summe ihrer beiden Vorgängerzahlen. Die Startzahlen sind 0 und 1.

Bildet man die Quotienten zweier benachbarter Fibonacci-Zahlen, tendieren die Quotienten zu einem Grenzwert, der als "goldener Schnitt" bekannt ist.

Viele Zapfen und spiralig angeordnete Blütenstände weisen -wie der Zapfen links- bezüglich der Anzahl der beiden Arten von Spiralen Fibonacci-Zahlen auf.

Gibt es eine Figur, die lediglich durch Drehen und Verschieben mit einem vergrösserten Bild derselben Figur zur Deckung gebracht werden kann?
Wie obige Abbildung zeigt, hat die logarithmische Spirale diese Eigenschaft: Die Ausgangsspirale oben rechts wird vergrössert; es entsteht die vergrösserte Spirale links.
Nun drehen wir die Ausgangsspirale um 180°; es entsteht die gelbe Spirale unten. Die gelbe Spirale ist deckungsgleich mit der vergrösserten Spirale.

Bemerkungen dazu:
-Man sagt, die Spirale sei selbstähnlich.
-Das Gesagte gilt natürlich nur, wenn man sich die Spirale "vollständig" denkt: Nach innen vollführt sie unendlich viele stets kleiner werdende Windungen, nach aussen macht sie unendlich viele stets grösser werdende Windungen. Das Gezeigte ist also nur ein kleiner Ausschnitt aus der unendlichen Spirale, die wir uns lediglich denken können. Diese unendliche Figur hat die Eigenschaft, deckungsgleich mit ihren sämtlichen Vergrösserungen und Verkleinerungen zu sein.