Die beurteilende Statistik (Inferenzstatistik) fragt nach der Zuverlässigkeit von Hypothesen und hilft, Schlüsse von Stichproben auf die Grundgesamtheit zu ziehen.
Kategoriale Skalen
- Nominalskala (Nomen = Name). Die Zahlen stehen nur als Abkürzungen für Begriffe und haben keinerlei rechnerische Bedeutung.
Beispiel: Zuordnung von Zahlen zu Berufen in einem Fragebogen:
1 = Koch, 2 = Konditor / Konditorin, 3 = ... - Ordinalskala (Rangordnung): Es ist kein Rechnen möglich, die Unterschiede zwischen den Zahlen haben keine reale Bedeutung ausser dass eine Rangordnung festgestellt wird.
Beispiel: Härteskala in der Mineralogie: 7 (Quarz) ist härter als 6 (Feldspat), usw.
Metrische Skalen
- Intervallskala: Die Unterschiede zwischen den Zahlen haben eine Bedeutung. Der Nullpunkt ist aber willkürlich gewählt.
Beispiel: Temperatur (in °Celsius oder °Fahrenheit): Die Differenzen sind bedeutsam, der Nullpunkt ist aber verschieden. Man kann nicht sagen, dass eine Temperatur von 20° C "doppelt so warm" bedeutet wie eine von 10° (der Engländer würde dem nicht zustimmen). - Verhältnisskala: Hier sind neben den Differenzen auch die Verhältnisse bedeutsam. Es gibt einen absoluten Nullpunkt.
Beispiel: Gewicht. Hier kann man (in jeder Gewichtseinheit) sagen, dass eine Person doppelt so viel wiegt wie eine andere.
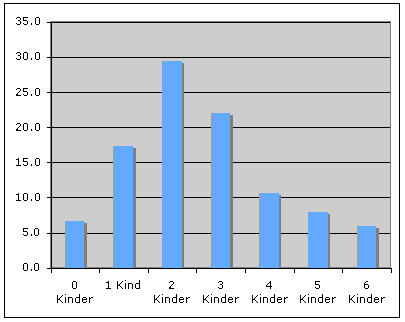 n = 150
n = 150
Darstellung der Daten aus dem Beispiel rechts in Form eines Balkendiagramms.
Höhe der Säule = Prozentanteil der Familien mit x Kindern.
Eine andere mögliche Darstellung wäre ein Kreis- oder Kuchendiagramm.
Die Grundgesamtheit n ist unbedingt anzugeben.
Beispiel: Merkmal X = Anzahl Kinder pro Familie in einer Siedlung von n = 150 Familien
| Merkmalswert xi | Besetzungszahl ni |
relative Häufigkeit hi |
relative Häufigkeit in % |
| x1 = 0 Kinder | n1= 10 Familien | 0.067 | 6.7% |
| x2 = 1 Kinder | n2= 26 Familien | 0.173 | 17.3% |
| x3 = 2 Kinder | n3= 44 Familien | 0.293 | 29.3% |
| x4 = 3 Kinder | n4= 33 Familien | 0.220 | 22.0% |
| x5 = 4 Kinder | n5= 16 Familien | 0.107 | 10.7% |
| x6 = 5 Kinder | n6= 12 Familien | 0.080 | 8.0% |
| x7 = 6 Kinder | n7= 9 Familien | 0.060 | 6.0% |
| n = 150 Familien | 1.000 | 100% |
Begriffe:
| Rohdaten, Urliste | Unpräparierte Daten, wie sie erfasst wurden. Sie werden in der Urliste festgehalten. |
| Stichprobe von Grösse n | Auswahl von n Merkmalsträgern aus einer Grundgesamtheit. |
| Merkmalsträger und Merkmal X | Im Beispiel oben sind die die Familien die Merkmalsträger. Das Merkmal X ist: "Anzahl Kinder pro Familie". |
| Merkmalswert xi | Wert des Merkmals X beim i-ten Merkmalsträger |
| diskretes Merkmal | Quantitatives Merkmal, das sich zählen lässt |
| stetiges Merkmal | Quantitatives Merkmal, das sich messen lässt |
| absolute Häufigkeit ni | Anzahl Elemente mit Merkmalswert xi |
| relative Häufigkeit hi | hi= ni / n = Bruchteil gemessen am Ganzen. Die Summe aller relativen Häufigkeiten ist 1. |
| relative Häufigkeit in % | (100⋅ni / n) % |
Literaturhinweise:
Bucher, Benno, Meier-Solfrian, Walter, Meyer, Urban, Schlick, Sandra: Statistik, Grundlagen, Beispiele und Anwendungen gelöst mit Excel, Compendio Bildungsmedien AG, Zürich, 1. Auflage, 2003
Gehring, Uwe W., Weins, Cornelia: Grundkurs Statistik für Politologen und Soziologen, VS Verlag für Sozialwissenschaften, Wiesbaden, 5. Auflage, 2009
Bemerkung zu statistischen Merkmalen:
Für Merkmale in der Statistik sollten Messvorschriften existieren, die festlegen, was genau man unter diesem Merkmal in der betreffenden Untersuchung verstehen will (Operationalisierung von Merkmalen). Was bedeutet etwa "Zufriedenheit am Arbeitsplatz", "Gerechte Vermögensverteilung", "Nachhaltigkeit eines Produkts", "Pünktlichkeit der SBB-Züge", usw.?
Je nach Definition eines Merkmals können nämlich die statistischen Resultate unterschiedlich ausfallen. So konnten z.B. im Juli 2020 die SBB
ihre Pünktlichkeits-Statistik verbessern, indem das Merkmal "Pünktlichkeit" einfach neu definiert wurde: Anstelle der Fahrgastpünktlichkeit wurde neu die Zugspünktlichkeit als Mass genommen. Ein voller Intercityzug mit Verspätung zählte früher viel mehr als ein verspäteter, fast leerer Regionalzug, weil viel mehr Personen von dieser Verspätung betroffen waren (diese Mess-Methode ist aus Kundensicht ja auch völlig plausibel). Neu zählt die Zugspünktlichkeit: Der verspätete Zug mit sehr vielen Passagieren zählt nun plötzlich mit gleichem Gewicht wie der verpätete leere Zug. Mit einem Schlag stieg so die Pünktlichkeit der Bahn...
Das Beispiel zeigt: Statistische Zahlen sind -auch wenn sie exakt erhoben werden- stets kritisch zu betrachten, indem man z.B. die Definition des gemessenen Merkmals gut anschaut.
Stetige Daten entstehen bei Messungen. Hier fasst man die Messwerte, die nahe beisammen liegen, zu Klassen zusammen.
Hier als Beispiel eine geordnete Liste von Geburtslängen in cm:
46.8 47.2 47.5 48.3 48.3 48.7 48.8 49.0 49.1 49.3
49.5 49.6 50.0 50.2 50.4 50.7 50.9 50.9 51.3 51.3
51.5 51.9 52.6 52.8 53.3 53.4 54.5 55.2
Um einen besseren Überblick zu gewinnen, bildet man nun "Klassen":
Beispiel:
Klasse 1: [46 cm; 48 cm[
Klasse 2: [48 cm; 50 cm[
Klasse 3: [50 cm; 52 cm[
Klasse 4: [52 cm; 54 cm[
Klasse 5: [54 cm; 56 cm[
Der Wert 48 cm gehört bereits zur Klasse 2; wir wählen also die Klassenintervalle hier rechts offen. (Es wäre auch möglich, die Intervalle links offen zu wählen.)
Faustregel für die Anzahl Klassen: √n, wobei n die Anzahl Messwerte ist. Hier wäre dieser Wert ≈ √28; wir könnten also 5 oder 6 Klassen bilden. Wir achten aber auf einigermassen sinnvolle Klassengrenzen. Zu viele Klassen schaffen keine Übersicht, zu wenig Klassen vereinfachen die Darstellung zu stark. Man muss einen sinnvollen Mittelweg finden.
Die Verteilung mit 5 Klassen (Klassenbreite = 2 cm) sieht nun wie folgt aus:
| Klasse | Klassenmittel / cm | ni = Anzahl Elemente in dieser Klasse: | Relative Häufigkeit hi |
| Klasse 1: | 47 cm | 3 | 0.107 |
| Klasse 2: | 49 cm | 9 | 0.321 |
| Klasse 3: | 51 cm | 10 | 0.357 |
| Klasse 4: | 53 cm | 4 | 0.143 |
| Klasse 5: | 55 cm | 2 | 0.071 |
Wir betrachten zunächst ein Balkendiagramm mit aneinanderstossenden Balken. Die Klassenbreite ist 2 cm. Die Höhen der Säulen geben die relativen Häufigkeiten an:
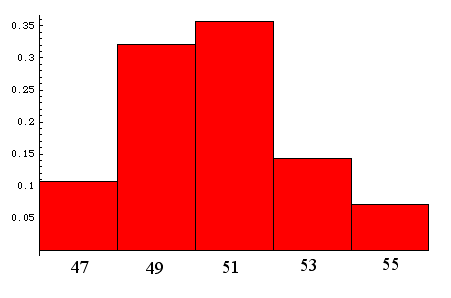
Die Häufigkeitsverteilung klassierter stetiger Daten kann aber vorzugsweise in einem Histogramm dargestellt werden [histion (griech.), Segel, Gewebe]. In einem Histogramm berühren sich die Balken ebenfalls. Die Säulenhöhe wird jedoch durch die Klassenbreite dividiert, sodass neu nicht mehr die Höhe der Balken, sondern die Balkenfläche die relative Häufigkeit angibt. Die y-Achse zeigt nun nicht mehr die relative Häufigkeit wie im Bild oben, sondern die relative Häufigkeit dividiert durch die Klassenbreite, also die Häufigkeitsdichte.
Im Vergleich zum Bild oben (Säulendiagramm) sind nun die Säulen im Histogramm unten nur noch halb so hoch (wegen der Klassenbreite 2):

Bild oben: Histogramm. x-Achse: Messwerte. Klassenbreite 2 cm (y-Achse: Häufigkeitsdichte = relative Häufigkeit dividiert durch Klassenbreite. Die Gesamtfläche des Histogramms ist 1 (oder 100%).
Mittelwert: Den Mittelwert ("Durchschnitt") der gemessenen Daten erhält man durch Aufsummieren aller Werte und Division durch n. Sind die Daten klassiert, kann der Mittelwert näherungsweise über die Klassenmittel bestimmt werden:
Mittelwert ≈ (3⋅47 + 9⋅49 + 10⋅51 + 4⋅53 + 2⋅55)/28 cm oder
Mittelwert ≈ (3⋅0.107 + 9⋅0.321 + 10⋅0.357 + 4⋅0.143 + 2⋅0.071) cm
Allgemein: Mittelwert = ∑ ni⋅hi
Zusammenfassung Histogramm: Die Normierung des Histogramms, derart, dass die gesamte rote Fläche gleich 1 wird, kann wie folgt geschehen: Man definiert folgende "Klassenfunktion":
|
Mittelwert
Mittelwert = ∑ ni⋅hi
Median
Der Median ist der mittlere Wert der nach Grösse geordneten Werteliste. Ein solcher mittlerer Wert existiert nur, wenn n ungerade ist. Für gerades n ist der Median der Durchschnitt der beiden mittleren Werte.
Beispiel der Geburtslängen (Liste oben): n = 28. Die mittlere Position liegt auf Rang 29:2 = 14.5. Der Median ist hier gleich (50.2 + 50.4):2 cm = 50.3 cm.
Vorgehen zur Bestimmung des Medians
- Die Daten werden nach Grösse geordnet.
- Medianrang = (n + 1) : 2
- n ungerade: Median = Wert mit dem berechneten Medianrang.
n gerade: Median = Durchschnitt der beiden dem berechneten Medianrang angrenzenden Werte.
Modus
Der Modus ist der am häufigsten vorkommende Wert. Er spielt in der Statistik keine grosse Rolle. Es können auch mehrere Werte gleich häufig vorkommen.
Beurteilung der Lagemasse
Der Mittelwert ist empfindlich gegenüber Ausreissern. Das bedeutet, dass extreme Werte am Rand der Verteilung den Mittelwert stark beeinflussen können. Oft lässt man deshalb Ausreisser bei der Berechnung des Mittelwerts weg (zur Definition von "Ausreissern" s. Abschnitt "Boxplot").
Der Median ist im Gegensatz zum Mittelwert robust gegenüber Ausreissern. Er hat dafür in der schliessenden Statistik andere Nachteile.
Welches Lagemass man am besten verwendet, muss im Einzelfall entschieden werden.

Zwei Maschinen produzieren Holzkugeln. Der Soll-Durchmesser sei 19.5 mm.
Um die Qualität der Maschinen zu beurteilen, entnimmt man von jeder Maschine eine Stichprobe von 10 Kugeln und misst die Durchmesser (Angaben in mm):
Maschine 1: 25 16 19 22 21 19 17 15 20 21
Maschine 2: 20 20 18 17 18 22 22 16 21 21
Welche Maschine arbeitet konstanter?
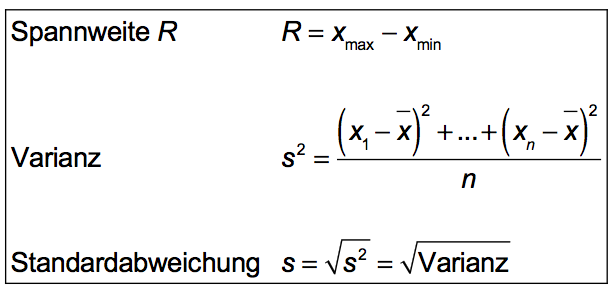
Formeln für die Streumasse
Das einfachste Streumass einer Datenverteilung ist die sogenannte Spannweite R ("Range"). R ist die Differenz zwischen dem grössten und dem kleinsten Wert.
Varianz und Standardabweichung werden im Beispiel rechts erklärt.
Die Streumasse drücken aus, in welcher "Stärke" die Daten um den Mittelwert herum streuen.
Die Formeln für diese drei Streumasse lauten:
Idee 1: Man ermittelt den Durchschnitt (Mittelwert). Resultat: Bei beiden Maschinen beträgt der Mittelwert 19.5 mm. Die Idee ermöglicht keinen Vergleich.
Idee 2: Man listet die Abweichungen vom Durchschnitt 19.5 mm auf und addiert sie:
Maschine 1: +5.5 -3.5 -0.5 +2.5 +1.5 -0.5 -2.5 -4.5 +0.5 +1.5. Summe = 0
Maschine 2: +0.5 +0.5 -1.5 -2.5 -1.5 +2.5 +2.5 -3.5 +1.5 +1.5. Summe = 0.
Fazit: Es ist gerade das Merkmal des Durchschnitts, dass die Summe der Abweichungen null ergibt. Auch diese Idee führt nicht zum Ziel.
Idee 3: Die Summe 0 in Idee 2 entstand wegen der Vorzeichen. Wir könnten die Absolutbeträge der Abweichungen nehmen und diese addieren:
Maschine 1: 5.5 3.5 0.5 2.5 1.5 0.5 2.5 4.5 0.5 1.5. Summe = 23.
Maschine 2: 0.5 0.5 1.5 2.5 1.5 2.5 2.5 3.5 1.5 1.5. Summe = 18.
Maschine 1: durchschnittliche absolute Abweichung vom Mittelwert: 2.3.
Maschine 2: durchschnittliche absolute Abweichung vom Mittelwert: 1.8.
Maschine 2 schneidet besser ab. Im Durchschnitt weicht sie pro Kugel um 1.8 mm (nach oben oder nach unten) vom Mittelwert ab.
Idee 4: Das Rechnen mit Absolutbeträgen ist kompliziert. Man bringt die Vorzeichen der Abweichungen auch weg, indem man die Abweichungen quadriert:
Maschine 1: 30.25 12.25 0.25 6.25 2.25 0.25 6.25 20.25 0.25 2.25.
Summe = 80.5. Durchschnitt pro Kugel: 8.05.
Maschine 2: 0.25 0.25 2.25 6.25 2.25 6.25 6.25 12.25 2.25 2.25.
Summe = 40.5. Durchschnitt pro Kugel: 4.05.
Maschine 2 hat die kleinere Abweichungszahl. Bei Idee 4 werden Abweichungen quadratisch "bestraft". Grössere Abweichungen werden also stärker gewichtet als kleinere. Die durchschnittliche quadratisch bestrafte Abweichung vom Mittelwert wird Varianz s2 genannt. Maschine 1 hat eine Varianz von 8.05, Maschine 2 eine solche von 4.05; sie arbeitet also mit weniger Schwankungen.*)
*) Dies ist nicht völlig gewiss, denn Maschine 2 könnte bei der Stichproben-Entnahme auch einfach "Glück" gehabt haben. Weitere Stichproben müssten die grössere Zuverlässigkeit von Maschine 2 bestätigen. Dies sind bereits Probleme der schliessenden Statistik: Wie kann von einer Stichprobe auf "das Ganze" geschlossen werden?
Bemerkung 1: Schliesst man von der Stichprobenvarianz auf die Varianz der Grundgesamtheit, wird in der Varianzformel links anstelle des Nenners n der Nenner n - 1 verwendet (Bessel-Korrektur), da die Formel mit Nenner n, die Varianz der Grundgesamtheit systematisch etwas zu tief schätzt. Genauere Begründung und Illustration dafür: hier.
Bemerkung 2: Da die Varianz eine quadrierte Grösse ist, stimmt die Einheit (hier mm2 ) nicht mit der ursprünglichen Einheit (mm) überein. Deshalb betrachtet man häufig die Wurzel aus der Varianz, also s. Diese Grösse wird Standardabweichung s genannt.
Eine gute Übersicht findet sich hier: http://de.wikipedia.org/wiki/Boxplot
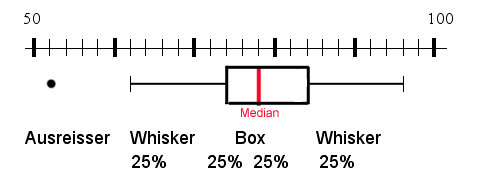
Der Boxplot gibt für quantitative Daten eine schnelle Übersicht über Lage und Verteilung. Die Daten werden zuerst nach Grösse sortiert. Das untere Quartil ist derjenige Wert, der an der Grenze zum untersten Viertel liegt. Der Median ist der mittlere Wert. Das obere Quartil liegt an der Grenze zum obersten Viertel.
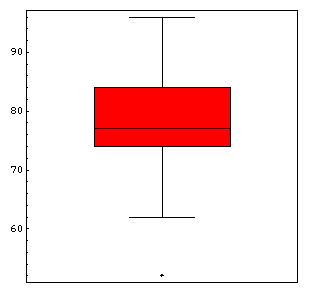
Beispiel: Prüfungspunkte in einer Klasse (n = 17):
76 74 82 96 62 76 78 72 52 86 84 76 78 92 82 74 88
Zuerst werden die Daten der Grösse nach geordnet:
52 62 72 74 74 76 76 76 78 78 82 82 84 86 88 92 96
Nun werden gemäss Tabelle rechts die Werte für den Boxplot bestimmt:
n = 17. Medianrang = (17 + 1) / 2 = 9 ⇒ Median = 78.
Rang unteres Quartil = (9 + 1) / 2 = 5 ⇒ unteres Quartil = 74
Rang oberes Quartil = 18 - 5 = 13 ⇒ oberes Quartil = 84
Minimum = 52, Maximum = 96
Interquartilsabstand = 84 - 74 = 10
oberer Zaun = 84 + 1.5⋅10 = 84 + 15 = 99. Maximum 96 innerhalb des Zauns.
unterer Zaun = 74 -
1.5⋅10 = 74 - 15 = 59. Zweitunterster Wert 62 ist noch innerhalb des Zauns. Der untere Whisker wird bis dorthin gezeichnet. Der kleinste Wert 52 ist ausserhalb des Zauns und folglich ein Ausreisser.
Man definiert also die Ausreisser wie folgt:
Hänge oberhalb und unterhalb der Box nochmals je die 1.5-fache Box an. Was ausserhalb liegt, zählt als Ausreisser. Diese Definition mit der anderthalbfachen Box ist reine Konvention.
Nun kann der Boxplot gezeichnet werden:
Hier der Boxplot wie er von einem Statistikprogramm erzeugt wird:
Formeln für die Erstellung eines Boxplots:
| Anzahl Werte | n |
| Medianrang | (n + 1) / 2 |
| Median | n gerade: Wert in der Rangmitte n ungerade: Durchschnitt der beiden rangmittleren Werte |
Rang unteres Quartil
|
Bemerkung: Die Quartilsränge werden z.T. auch leicht anders berechnet. Viele Taschenrechner gehen so vor: n gerade: Nimm von jeder Datenhälfte wieder den mittleren Wert. n ungerade: "Entferne" in Gedanken den Median und nimm von den verbleibenden Reststücken wieder den mittleren Wert. |
| Unteres Quartil qu | Wert auf dem unteren Quartilsrang bzw. Durchschnitt der beiden angrenzenden Werte |
| Rang oberes Quartil | (n + 1) minus Rang unteres Quartil |
| Oberes Quartil qo | Wert auf dem oberen Quartilsrang bzw. Durchschnitt der beiden angrenzenden Werte |
| kleinster Wert | |
| grösster Wert | |
| Interquartilsabstand dq | qo - qu = oberer Quartilswert minus unterer Quartilswert = Spannweite der Box. |
| oberer Zaun fo | qo + 1.5 dq |
| unterer Zaun fu | qu - 1.5 dq |
| Ausreisser | Werte ausserhalb der Zäune |
Bemerkungen zum Boxplot:
Die Ausreisser werden als Einzelwerte eingezeichnet.
Die Whisker (Antennen) [whisker, engl: Schnurrhaar] umfassen das unterste und das oberste Viertel der Verteilung ohne die Ausreisser.
Die Box umfasst die beiden mittleren Viertel.
In die Box hinein wird der Median eingetragen.
Die Boxplots werden in den meisten Fällen senkrecht gezeichnet.
Boxplots eigenen sich vorzugsweise zum Vergleich mehrerer Datenreihen (man könnte also z.B. mehrere Klassen in Bezug auf die gleiche Prüfung vergleichen).
Ein Boxplot zeigt auf einfache Art und Weise Lage und Verteilung der Daten. Die Länge der Box und die Länge der Whiskers zeigen die Stärke der Streuung, der Median zeigt die Lage.
Weitere Werte (nicht zum Boxplot gehörend):
Mittelwert: 78.1 Punkte. Varianz = [ ∑ ( xi - 78.1)2 ] / 16 = 110.2 ⇒
Standardabweichung s = 10.5 Prüfungspunkte.
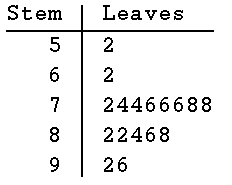
Stängel-Blatt-Diagramm
Eine rasche Übersicht vermittelt auch ein Stem-Leave-Plot: Die Zehner bilden den Stamm, die Einer die Blätter. Hier ein Beispiel mit denselben Daten:
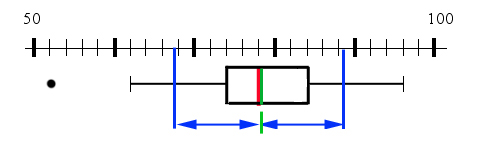
Rot: Median, grün: Mittelwert. Die Werte sind hier fast gleich gross.
Blau: Mittelwert ± s, d.h. 78.1± 10.5. Der blaue Bereich umfasst also das Intervall [67.6;88.6]. Für normalverteilte Daten befinden sich in diesem Bereich ca. 68% der Daten. In unserem konkreten Beispiel sind es 13/17 der Werte, das sind ca. 76.5%.
Interpretation der Standardabweichung s
Bei einer Normalverteilung (symmetrische Glockenverteilung) befinden sich
- im Bereich "Mittelwert ± s" ca. 68% der Daten
- im Bereich "Mittelwert ± 2s" bereits ca. 95% der Daten
- im Bereich "Mittelwert ± 3s" ca. 99.7% der Daten.
Bei einer beliebigen (nicht unbedingt symmetrischen) Verteilung kann man nicht so viel sagen. Die Formel von Tschebyschev besagt: Es befinden sich
- im Bereich "Mittelwert ±2s" mindestens 75% der Daten
- im Bereich "Mittelwert ± 3s" mindestens 89% der Daten.
Wir betrachten nochmals die empirische Häufigkeitsverteilung von Beispiel 10.2.:
X = Anzahl Kinder pro Familie.
Der Wert "xi Kinder" komme ni-mal vor.
Allgemein haben wir:

Dann berechnet sich der Mittelwert (Durchschnitt) wie folgt:
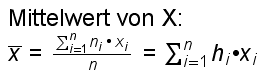
Die Varianz ist die durchschnittliche quadratische Abweichung vom Mittelwert (wir nehmen an, n sei gross, so dass wir statt durch (n - 1) ohne grosse Abweichung auch durch n dividieren können):
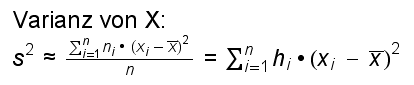
Nun betrachten wir eine Zufallsvariable X aus einem Glücksspiel (Beispiel: X = Anzahl Einsen beim Würfeln mit n Würfeln). Der Wert xi komme mit Wahrscheinlichkeit pi vor.
In Analogie zur Situation in der linken Spalte können wir auch hier eine mittlere Erwartung und eine Varianz berechnen. Die Wahrscheinlichkeit pi ist die relative Häufigkeit auf lange Sicht (bei sehr vielen Würfen). An die Stelle von hi tritt also hier einfach pi . An die Stelle des Mittelwerts tritt der sogenannte Erwartungswert E(X) oder μX . Er sagt, mit welchem Durchschnittswert von X wir bei sehr vielen Würfen (n sehr gross) rechnen müssen.
Die Analogie sieht also so aus:

Die Formeln für Erwartungswert und Varianz einer Wahrscheinlichkeitsverteilung lauten demnach:
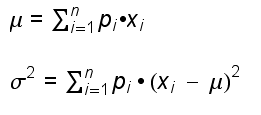
Erwartungswert und Varianz der Binomialverteilung
μ = n ⋅ p
σ2 = n⋅p⋅(1 - p)
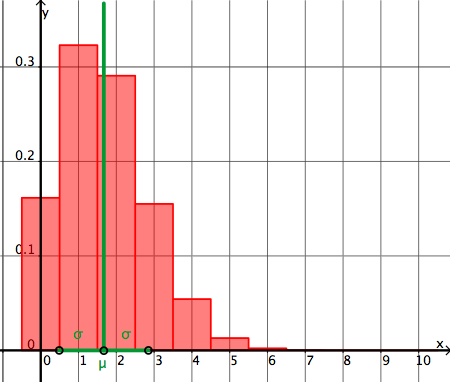
Beispiel rechts: Würfeln mit 10 Würfeln. Zufallsvariable X: "Anzahl gewürfelte Einsen".
Erwartungswert und Varianz von X:
μ = 10 ⋅ (1/6) ≈ 1.67.
σ2 = 10 ⋅(1/6)⋅(5/6) ≈ 1.39
σ ≈ 1.18
12. Wir testen eine Werksgarantie
Vorbemerkung:

Die Säulendiagramme zeigen die Wahrscheinlichkeiten p(x), beim Würfeln mit n Würfeln x-mal eine Eins zu würfeln. Mit wachsendem n verschiebt sich der Erwartungswert μ nach rechts und die Verteilung wird zunehmend breiter und flacher. Dies liegt daran, dass bei gleich bleibender Streifenbreite die Diagrammfläche konstant bleibt. Wählt man die Streifenbreite = 1, so ist die gesamte Fläche aller Streifen zusammen gleich 1 (Summe aller Teilwahrscheinlichkeiten = 1).
Man erkennt die zunehmende Symmetrisierung der Verteilung.
Geogebramodell Binomialverteilung
Die Binomialverteilung nähert sich mit wachsendem n einer symmetrischen, glockenförmigen Verteilung, einer sogenannten gaussschen Normalverteilung an.
Für eine gausssche Normalverteilung gilt:
- Im Intervall [μ - σ, μ + σ] befinden sich ca. 68% aller Daten.
- Im Intervall [μ - 2σ, μ + 2σ] befinden sich ca. 95.4% aller Daten.
Für σ2 = n⋅p⋅(1 - p) > 9 kann eine Binomialverteilung durch eine Normalverteilung angenähert werden, für welche obige Regeln gelten.
Dies wenden wir nun an, um eine Werksgarantie zu testen:
| Ein Glühbirnenhersteller garantiert, dass 98% der ausgelieferten Ware einwandfrei sei. Bei einem Test von 1'000 Birnen waren 32 defekt. Ist das ein Widerspruch zur Werksangabe? |
Lösung:
Es ist n = 1'000 und p("Birne in Ordnung") = 0.98.
Daraus ergibt sich
μ = n ⋅ p = 980 und σ2 = n⋅p⋅(1 - p) = 19.6 und σ ≈ 4.4.
Die Bedingung für die Näherung durch die Normalverteilung ist gegeben, d.h. das Histogramm unten entspricht ziemlich gut einer gaussschen Glockenverteilung (man erkennt nur noch leichte Asymmetrien beim genaueren Hinsehen; die Verteilung ist noch ein ganz klein wenig linksschief; Säulen von vernachlässigbarer Höhe würden ja noch bis 0 gehen).
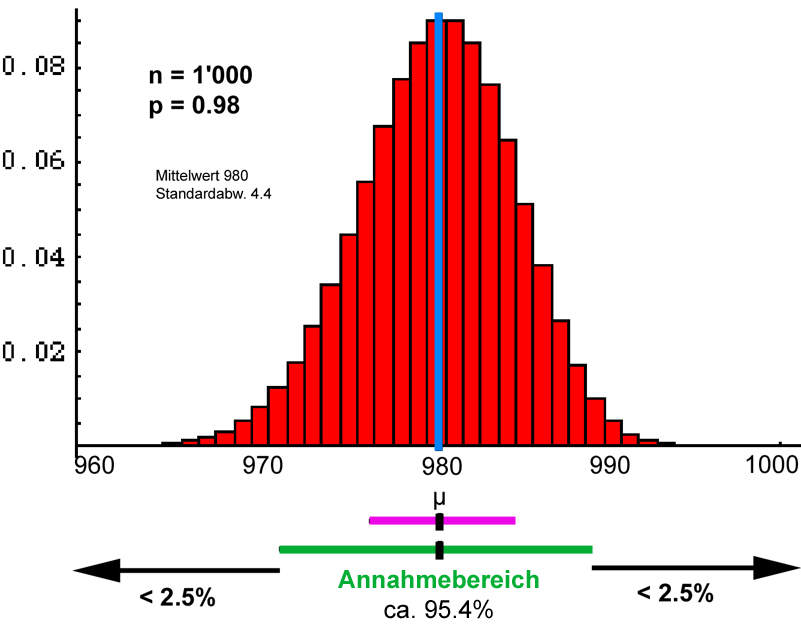
Im Bereich [980 - 2⋅4.4; 980 + 2⋅4.4] = [971,2; 988.8] befinden sich ca. 95.4% aller Stichprobenresultate, d.h. in 95.4% der gemachten Stichproben erwarten wir zwischen 972 und 988 funktionierende Birnen. In weniger als 2.5% der Stichproben erwarten wir Anzahlen ≤ 971, ebenso erwarten wir in weniger als 2.5% der Stichproben Anzahlen ≥ 989; diese Fälle sind also - sofern die Werksbedingungen zutreffen - sehr unwahrscheinlich.
Wir fanden in unserer Stichprobe nur 968 funktionierende Birnen. Eine solche Stichprobe zu ziehen ist unter Voraussetzung der abgegebenen Werksgarantie eher unwahrscheinlich. Somit zweifeln wir diese an.
Wir benutzen das Intervall [μ - 2σ, μ + 2σ] als Annahmebereich (in der Grafik grün markiert): Liegt unser Stichprobenwert innerhalb dieses Intervalls, vertrauen wir der Werksgarantie. Liegt das Resultat unterhalb dieses Intervalls, zweifeln wir die Garantie an. (Theoretisch wäre es allerdings möglich, dass auf sehr unwahrscheinliche Art und Weise trotz eingehaltener Werksgarantie eine solch tiefe Anzahl korrekter Birnen in einer Stichprobe auftreten könnte; die Wahrscheinlichkeit dafür ist jedoch < 2.5%, d.h. wir prangern die Firma vermutlich zu Recht an.)
Bemerkungen zu obigem Test
Für σ2 = n⋅p⋅(1 - p) > 9 können wir bei einer Binomialverteilung die Regeln für Normalverteilung anwenden. Das Intervall [μ - 2σ, μ + 2σ] ist der 95.4%-Annahmebereich.
Häufig benutzt wird das 95%-Intervall [μ - 1.96σ, μ + 1.96σ].
Auf jeden Fall sehen wir, dass die Standardabweichung σ als Mass dessen benützt wird, was noch als (je nach Kontext) "normale", "annehmbare" Abweichung gilt.
Warum sagt eine Abweichung vom Mittelwert allein noch nicht viel aus?
Nehmen wir als Beispiel die Körpergrösse von Menschen: Ist eine Abweichung von 7 cm vom Mittelwert viel oder wenig, auffällig oder nicht auffällig? Die Antwort hängt von der Streuung der Körpergrösse in der Gesamtbevölkerung ab.
Stellen wir uns eine Population vor, bei der alle Individuen praktisch dieselbe Körpergrösse haben. Die Standardabweichung als Streumass wäre dort sehr klein. Eine Abweichung von 2 cm vom Mittelwert wäre dort schon sehr auffällig, während dies bei uns noch völlig unauffällig ist. Was punkto Auffälligkeit bzw. Unauffälligkeit zählt, ist die Frage: Um welchen Faktor der Standardabweichung weicht eine Körpergrösse vom Mittelwert ab?
Für die Normalverteilung besagt eine Abweichung von einer Standardabweichung vom Mittelwert nach unten, dass die Person sich ungefähr an der Grenze zum kleinsten Sechstel der Bevölkerung befindet. Eine Abweichung von 1 σ vom Mittelwert nach oben bedeutet, dass sich die Person etwa an der Grenze zum obersten Sechstel der Bevölkerung befindet. Dazwischen liegen die 2/3 der "unauffälligen Durchschnittspersonen". Abweichungen von 2σ sind bereits sehr auffällig: Nur noch etwa 1/40 der Bevölkerung zeigt extremere Werte.
Link: Eine sehr übersichtliche Zusammenfassung der deskriptiven Statistik:
Prof. Dr. Burkhardt Seifert, Universität Zürich: Crashkurs Biostatistik:
http://www.biostat.uzh.ch/teaching/crashcourse/biostatistics.html
Dort PDF "Deskriptive Statistik" anwählen.
Körpergrössen in der Schweiz (Quelle: s. Link Prof. Dr. Burkhardt Seifert, UZH, linke Spalte):
| Geschlecht | Mittelwert / cm | Standardabweichung / cm |
| m | 180.20 | 6.233 |
| w | 167.22 | 6.568 |
a) Ermitteln Sie das 68%-Intervall.
b) Ermitteln Sie das 95.4%-Intervall.
Lösungen:
a) männlich: 180.20 ± 6.233 → [173.967, 186.433]
weiblich: 167.22 ± 6.568 → [160.652, 173.788]
a) männlich: 180.20 ± 12.466 → [167.734, 192.666]
weiblich: 167.22 ± 13.136 → [154.084, 180.356]
Die Ungleichung von Tschebyscheff
Eine heuristische Herleitung hier.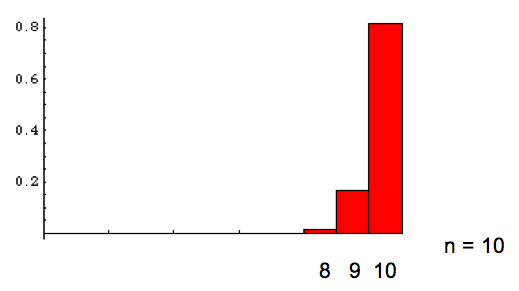
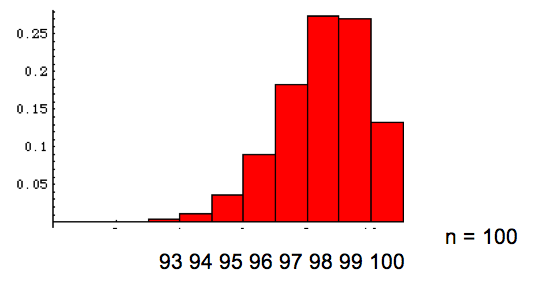
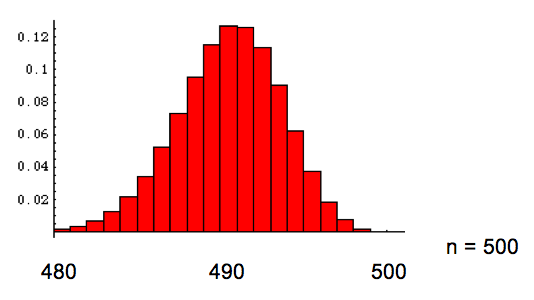
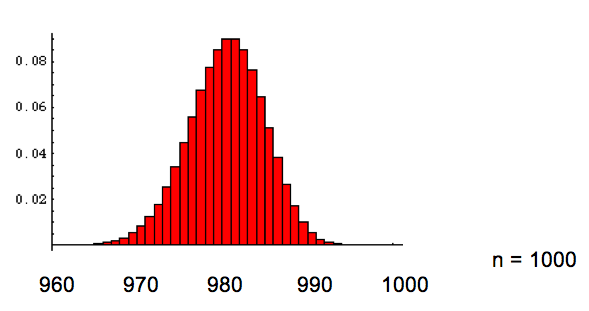

Die Werksgarantie für ausgelieferte Teile laute:
98% der ausgelieferten Teile sind garantiert einwandfrei: p("in Ordnung") = 0.98.
Oben sehen wir die Histogramme für Stichproben der Grösse n = 10, n = 100, n = 500 und n = 1'000. Wir sehen, dass mit wachsender Stichprobengrösse die Verteilung sich einer gaussschen Normalverteilung annähert, für die wir die "Gaussregeln für Normalverteilung" anwenden dürfen (siehe Spalte links).
Im Beispiel mit p = 0.98 ist die Bedingung n⋅p⋅(1-p) > 9 für n > 459 erfüllt.
Der 95.4%-Annahmebereich für eine Stichprobe der Grösse n = 500 ist
[490-3.1, 490+3.1] ≈ [487, 493]. Finden wir in einer Stichprobe der Grösse 500 mehr als 493 funktionierende Teile, vermuten wir, dass die Werksgarantie sogar noch übertroffen wird. Finden wir weniger als 487 funktionierende Teile, zweifeln wir an der Garantie. Dabei haben wir hier das 95.4%-Annahmeintervall gewählt. Auf welchem "Niveau" man vertraut, muss stets angegeben werden.
Die Firma im Beispiel oben gibt diesmal keine Werksgarantie ab. Aufgrund entnommener Stichproben wollen wir jedoch trotzdem die uns unbekannte Produktionszuverlässigkeit, also den Prozentsatz korrekter Teile, zu ermitteln. Wir versuchen also, p("korrekt") abzuschätzen.
Wir wählen wieder eine Stichprobe der Grösse n = 1000.
Nehmen wir als Beispiel an, wir fänden in der Zufallsstichprobe 970 korrekte Teile. Welche Werksgarantie würde zu diesem Ergebnis passen?
Wählen wir einmal versuchsweise eine Werksgarantie von p = 0.98. Wir erhalten mit diesem p einen Mittelwert von 1000⋅0.98 = 989 und eine Standardabweichung von (1000⋅0.98⋅0.02)1/2 = 4.43. Wir wählen den 95%-Annahmebereich, d.h. bilden das Annahmeintervall
[998 - 1.96⋅4.43 , 998 + 1.96⋅ 4.43] = [989.3 , 1006.7].
Werte > 1000 sind nicht möglich, das Annahmeintervall ist somit
[989.3 , 1000]. Wir müssten also bei einer Werksgarantie von p = 0.98 eine Anzahl von 990 oder mehr korrekten Teilen finden; dies würden wir bei 95% der Stichproben erwarten. Wir fanden jedoch nur 970 korrekte Teile.
Unsere Annahme p = 0.98 ist also mit grosser Wahrscheinlichkeit zu hoch angesetzt.
Die Frage lautet nun: Welche p können wir annehmen, um den Stichprobenwert 970 im Annahmebereich [μ -1.96σ , μ + 1.96σ] vorzufinden?
Wir suchen diejenigen Werte von p, bei denen 970 gerade noch auf dem linken und auf dem rechten Rand des Intervalls liegt:
970 = μ - 1.96σ
970 = μ + 1.96σ
oder
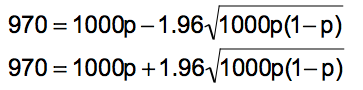
Diese beiden Gleichungen, aufgelöst nach p, ergeben:
p = 0.979 bzw. p = 0.957.
Die gesuchte Werksgarantie, d.h. das gesuchte p("korrekt"), liegt also mit 95%-iger Wahrscheinlichkeit zwischen den Werten 0.957 und 0.979.
Das Intervall [0.957 , 0.979] ist das durch unsere Stichprobe (k = 970 Treffer) gefundene 95%-Vertrauensintervall für die gesuchte Wahrscheinlichkeit p("korrekt").
Jede entnommene Stichprobe ergibt ein leicht anderes Vertrauensintervall. Bei 95% der so berechneten Vertrauensintervalle erwarten wir eine Überdeckung des wirklichen Wahrscheinlichkeitswertes, d.h. der wirklichen, aber uns unbekannten Werksgarantie.
Im folgenden Geogebra-Applet werden Vertrauensintervalle berechnet: Man entnimmt eine Stichprobe der Grösse n = 1000 und ermittelt die Anzahl k der korrekten Teile (der "Treffer"). Mittels des Schiebereglers wird k eingestellt. Das Applet zeigt dann das Vertrauensintervall, welches mit 95%-iger Wahrscheinlichkeit den wirklichen Wert von p überdeckt.
Geogebra-Applet zur Berechnung des Vertrauensintervalls für p.
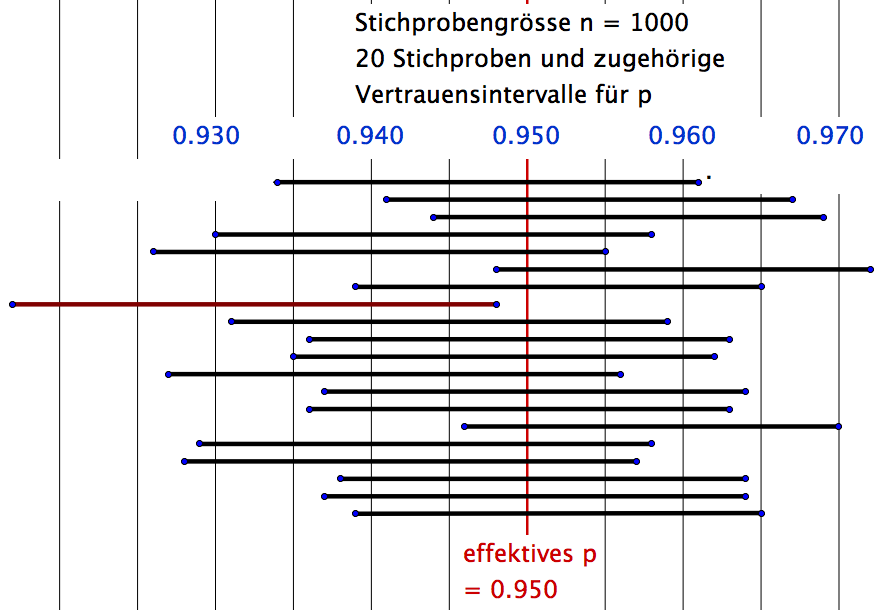
Entnahme von 20 Stichproben der Grösse n = 1000 bei einer wirklichen Werkszuverlässigkeit von p("korrekt") = 0.950. Normalerweise kennt man das wirkliche p nicht und schätzt ein Vertrauensintervall aufgrund der Stichprobe. Bei den 95%-Vertrauensintervallen erwarten wir, dass etwa 19 von 20 Stichproben Intervalle liefern, die den wirklichen Wert von p überdecken. Rot markiert ein "Ausreisser-Intervall". Hätten wir nur diese eine Ausreisser-Stichprobe gezogen, würden wir das wahre p falsch schätzen. Eine solche Ausreisser-Stichprobe ist jedoch selten.
Rechts: Konfidenzellipse
Stichprobengrösse n = 1000
waagrechte Achse: k = Anzahl korrekt vorgefundener Teile in der Stichprobe
senkrechte Achse: "wirkliche" Wahrscheinlichkeit p("korrekt")
Die Ellipse begrenzt das 95%-Vertrauensintervall für p("korrekt").
Die Darstellung wird oft auch mit vertauschten Achsen abgebildet.
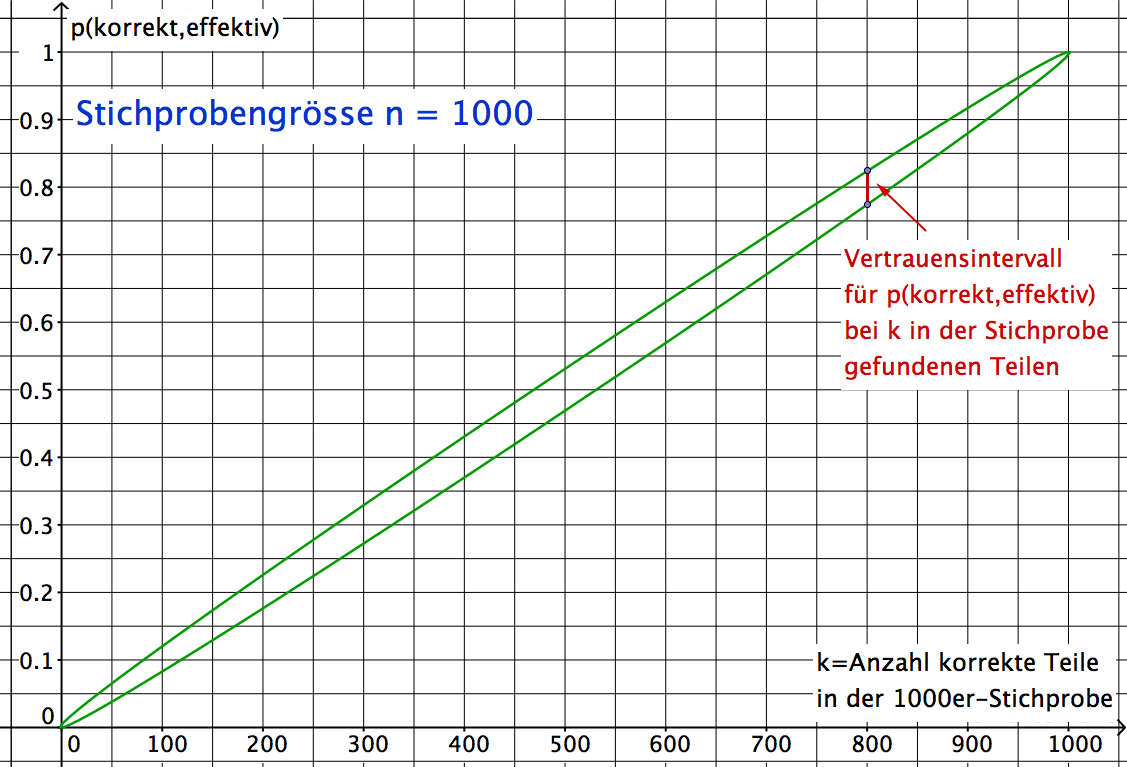
Sei wieder p("korrekt") unbekannt. Wir finden in der Stichprobe der Grösse n den relativen Anteil h = x / n an korrekten Teilen. Es ist p = μ / n.
Das 95.4%-Annahmeintervall für x korrekte Teile in der Stichprobe ist
[ μ - 2σ, μ + 2σ] =
[ μ - 2(n⋅p⋅(1-p))1/2 , μ + 2(n⋅p⋅(1-p))1/2 ].
Das entsprechende Intervall für x / n = h und p = μ / n erhalten wir, indem wir durch n dividieren:
[p - 2(p(1-p))1/2 / n1/2 , p + 2(p(1-p))1/2 / n1/2 ].
Wir dehnen dieses Intervall noch etwas aus, indem wir den maximal möglichen Wert für p(1-p) wählen, der für p = 1/2 entsteht. p(1-p) wird dann 1/4, die Wurzel daraus 1/2. Das so vergrösserte Intervall wird dann
[p - 1/√n , p + 1/√n].
Mit mehr als 95%-iger Wahrscheinlichkeit liegt also h im Intervall
[p - 1/√n , p + 1/√n] oder -umgekehrt gesprochen, da wir ja h kennen und p unbekannt ist:
Mit mehr als 95%-iger Wahrscheinlichkeit wird das wahre, aber uns unbekannte p durch das sogenannte Vertrauensintervall [h - 1/√n , h + 1/√n] eingefangen.
Beispiel 1: Wir nehmen noch einmal dasselbe Beispiel wie oben ("Schätzung einer unbekannten Wahrscheinlichkeit") und schätzen diesmal mit der "Faustformel":
N = 1000. Gefundene korrekte Teile: 970 => h = 0.97.
Mit mehr als 95%-iger Wahrscheinlichkeit wird das wahre (unbekannte) p eingefangen vom Intervall [0,97 - 1/√1000, 0.97 + 1/√1000] =
[0.97 - 0.03, 0.97 + 0.03] = [0.94, 1] = [94%, 100%].
Man sieht, dass diese "Faustschätzung" gröber ist als die genauere Schätzung oben, welche ein engeres 95%-Vertrauensintervall von [95.7%, 97.9%] ergab.
Die 1/√n-Faustformel lässt eine überschlagsmässige, schnelle Abschätzung zu, liefert jedoch ein etwas zu grosses Intervall.
Beispiel 2: Ein Politiker möchte durch eine Umfrage die Wahrscheinlichkeit p für seine Wiederwahl abschätzen. Er befragt 1000 Personen. 540 Personen geben an, ihn wählen zu wollen. Welches Vertrauensintervall (Niveau mind. 95%) ergibt die Faustformel?
Lösung:
[0.54 - 0.03, 0.54 + 0.03] = [51%, 57%]. Falls die Umfrage repräsentativ war, kann er also mit mehr als 95%-iger Wahrscheinlichkeit mit einer (ev. knappen) Wiederwahl rechnen.