Analysis of Variance (ANOVA) ist eine statistische Methode, um Differenzen mehrerer Mittelwerte zu testen. Dies geschieht durch die Analyse von Varianzen.
Beispiel:
Man testet vier verschiedene Trainingsmethoden, A, B, C, D, zur Förderung der Beweglichkeit bei Personen im Alter zwischen 70 und 75.
Am Schluss der Trainingskurse wird ein Beweglichkeitstest durchgeführt, der zu einer Gesamtpunktezahl führt. In jeder Gruppe seien 13 Personen.
Die Nullhypothese lautet: Die Kurse unterscheiden sich nicht, d.h. die Mittelwerte des Schlusstests sind bei allen Gruppen ungefähr gleich.
Begriffe:
Abhängige Variable: Das untersuchte Merkmal, im Beispiel oben die Punktezahl im Beweglichkeitstest. Das Skalenniveau dieser Variablen muss metrisch sein.
Unabhängige Variable, auch Faktor genannt: Im Beispiel oben das Beweglichkeitstraining. Die Faktoren müssen kategorial gestuft sein, im Beispiel: Trainingsmethoden A, B, C, D.
Wird der Einfluss eines einzigen Faktors untersucht, spricht man von einfaktorieller Varianzanalyse. Damit eine solche sinnvoll ist, muss sichergestellt sein, dass nicht andere, unberücksichtigte Faktoren hineinspielen und das Ergebnis unkontrolliert verfälschen. Der Faktor "Beweglichkeitstraining" in seinen vier unterschiedlichen Behandlungsarten A, B, C und D wird Treatmentfaktor genannt.
Grundidee der einfaktoriellen Varianzanalyse*):
Die Varianz der Punktezahlen wird auf zwei Arten geschätzt:
a) Streuung der Punktezahlen unabhängig davon, ob die Nullhypothese gültig ist oder nicht (Mean squared Error MSE), d.h. Varianz aufgrund zufälliger oder störender Einflüsse (Fehlervarianz). In unserem Beispiel: Varianz durch die natürliche unterschiedliche Beweglichkeitskonstitution unserer Probanden, die bereits zufällig gegeben ist, unterschiedliche Tagesform, individuelle Motivation, usw. Das ist die Streuung ohne Einfluss der Trainingsmethode.
Wir nehmen dafür den Mittelwert der Varianzen der einzelnen Gruppen
Warum nimmt man nicht die totale Varianz aller 52 Daten? - Weil dort eine allfällige Wirkung der Trainingsmethode einfliesst! Im MSE-Wert hingegen ist dieser Effekt nicht dabei! Er ist der Varianz-Schätzer ohne Treatmenteffekt.
b) Streuung basierend auf der Gruppenmittelwert-Streuung (MSB-Wert = Mittelwertvarianz multipliziert mit Gruppengrösse; B steht für between Groups).
Wir tun hier also so, als ob es innerhalb jeder Gruppe keine Streuung gäbe und alle Mitglieder gemäss dem Gruppenmittelwert abgeschlossen hätten.
Die Streuung der Mittelwerte kommt zustande durch die natürliche Streuung der Mittelwerte bei Stichproben (hier 4 Stichproben à je 13 Personen) plus eine allfällige Wirkung der Trainingsmethode.
| *) Diese Einführung mit der Schätzung von MSE und MSB ist übernommen aus: David M. Lane: An Introduction to Statistics - an interactive E-Book Kapitel 15, Analysis of Variance Vgl. auch dieses Open Textbook Das illustrierende Beispiel entstammt nicht diesem Buch und ist erfunden. |
Sind die Gruppenmittelwerte signifikant verschieden, ist also die Nullhypothese nicht richtig, wird die Varianz-Schätzung via MSB grösser ausfallen als diejenige via MSE, denn die natürliche Streuung der Mittelwerte durch die Stichprobenwahl wird dann durch die unterschiedliche Wirkung der Trainingsarten A, B, C, D noch verstärkt.
Gilt hingegen die Nullhypothese, hat also die Trainingsmethode keinen Einfluss, wird der MSB-Wert ungefähr dem MSE-Wert entsprechen; beide Werte schätzen dann (auf zwei verschiedene Berechnungsarten) die Varianz ohne Methodeneinfluss.
Ist aber MSB erheblich grösser als MSE, kann geschlossen werden, dass mindestens zwei Trainingsmethoden sich voneinander signifikant unterscheiden; die Nullhypothese wird dann abgelehnt.
Wichtig:
ANOVA kann nicht sagen, welches Training anders wirkt! (Vgl. dazu die Anmerkung am Schluss.) Auch über "besser" oder "schlechter" wird nichts entschieden. Das Resultat ist also relativ schwammig und besagt nur: Mindestens zwei Methoden unterscheiden sich signifikant.
Voraussetzungen für ANOVA:
1) Die Gruppen müssen etwa gleiche Varianz haben. (Es darf also in unserem Beispiel nicht eine Gruppe einseitig aus ehemaligen Tänzerinnen und Tänzern bestehen.) Diese Voraussetzung kann mit einem Levene-Test sichergestellt werden. Die Gruppen unseres Beispiels sollten z.B. per Zufallsauswahl gebildet werden.
Wir nehmen hier auch an, dass die Trainingsmethode die Gruppenvarianz nur unbedeutend oder gar nicht verändert, obwohl solche Effekte durchaus auftreten können: Es könnte z.B. ein Beweglichkeitstraining vorwiegend die unbeweglicheren Personen fördern und die sehr beweglichen unterfordern, was vermutlich die Streuung verkleinern würde; oder es könnte ein Training nur auf die beweglicheren Personen abzielen und die andern überfordern, was dann ev. die Streuung erhöhen würde (die Beweglichen würden noch besser, die andern blieben auf gleich tiefem Niveau). Wir kennen solche Effekte auch aus dem Bildungsbereich, wenn eine Lehrmethode vorwiegend auf eine bestimmte Lernenden-Subgruppe zugeschnitten ist und die übrigen Lernenden "abhängen".
2) Die Gruppen müssen (in unserem Beispiel punkto Beweglichkeit) einer Normalverteilung genügen.
3) Jeder Ergebniswert ist unabhängig von den andern Ergebniswerten. (Jede Person erhält in unserem Beispiel genau eine Schlusspunktezahl, für die nur sie allein verantwortlich ist.)
Auch dies ist nicht immer selbstverständlich. Es könnten gruppendynamische Effekte eine Rolle spielen, welche die Testergebnisse "querbeeinflussen". Eine gute und motivierende Gruppenatmosphäre kann z.B. den Gruppenmittelwert im abschliessenden Beweglichkeitstest positiv beeinflussen; wenn alle sich anstrengen, strenge ich mich selber auch an und erreiche mehr Punkte. Damit würden weitere Faktoren hereinspielen, und der ursprünglich vielleicht rein methodentechnisch geplante Vergleich der Trainingsmethoden würde dadurch fragwürdig.
Man sieht: Es geht nie nur um Statistik, sondern ebenso sehr um eine umsichtige Versuchsplanung, Durchführung und Interpretation.
Man kann noch so klug statistisch rechnen: Die Ergebnisse werden fragwürdig, wenn Einflüsse ausser Acht gelassen werden, die relevant wären, in unserem Beispiel vielleicht die Übungsatmosphäre im Gruppentraining, die ebenfalls ein relevanter Faktor wäre, oder die Person, die das Training leitet. Für einen solchen Einbezug mehrerer Faktoren gibt es die multifaktorielle Varianzanalyse.
Die Ergebnisse unseres (konstruierten) Beispiels seien wie folgt:
| Trainingsmethode | Punktemittelwert der Gruppe | Varianz |
| A | 13.4 | 9.5 |
| B | 12.3 | 8.6 |
| C | 12.3 | 7.1 |
| D | 10.0 | 7.0 |
| Mittelwert der Spaltendaten | 12.0 | 8.05 |
Wir haben k = 4 Gruppen (Stufen) mit je gleicher Anzahl n = 13 teilnehmender Personen, also total k⋅n = N = 52 Versuchspersonen.
MSE-Wert:
Wir schätzen die Varianz durch das Mittel der Gruppen-Varianzen. Wir finden MSE = 8.05. Man sieht sofort, dass in dieser Rechnung die Streuung der Gruppenmittelwerte und damit auch die Behandlungsmethode (A, B, C oder D) keine Rolle spielt.
MSB-Wert:
Wir wissen, dass die Stichproben-Mittelwerte schwächer streuen als die Grunddaten.
Die Varianz σM2 der Mittelwerte ist σM2 = σ2 / n oder σ2 = n⋅ σM2 .
Wir schätzen σM2 durch die Varianz der empirisch erhaltenen Gruppenmittelwerte, die sich im Beispiel links zu 2.05 errechnet (Varianzformel mit Nenner 3). Um MSB zu bestimmen, multiplizieren wir diesen Wert mit n = 13 und erhalten MSB = 26.65. In diesen Wert fliesst nun ein allfälliger Unterschied in der Wirkung der Varianten A, B, C und D ein.
Hätte das Treatment überhaupt keine Wirkung, wäre die Varianz der Gruppenmittelwerte (4 Stichproben à 13 Personen) in einem gewissen Streubereich um 0.6 herum, also sehr klein, und MSB wäre dann im Bereich um 8 herum, also etwa gleich wie MSE. In unserem Beispiel ist im Fall keiner Treatmentwirkung mit etwa 60% Wahrscheinlichkeit MSB sogar kleiner als MSE.
Nun bilden wir den Quotienten MSB : MSE = 26.65 : 8.05 = 3.31.
Dies ist der Fisher-Quotient, unsere Prüfgrösse.
Rechts: Die Ergebnisse unseres Beispiels (Tabelle oben) grafisch.
Sind mindestens zwei Mittelwerte signifikant verschieden oder nicht?
Ein Treatment-Einfluss ist umso wahrscheinlicher, je schmaler die Glockenkurven der Gruppen sind (MSE klein) und je grösser die Varianz der Mittelwerte ist (ergibt grosses MSB).
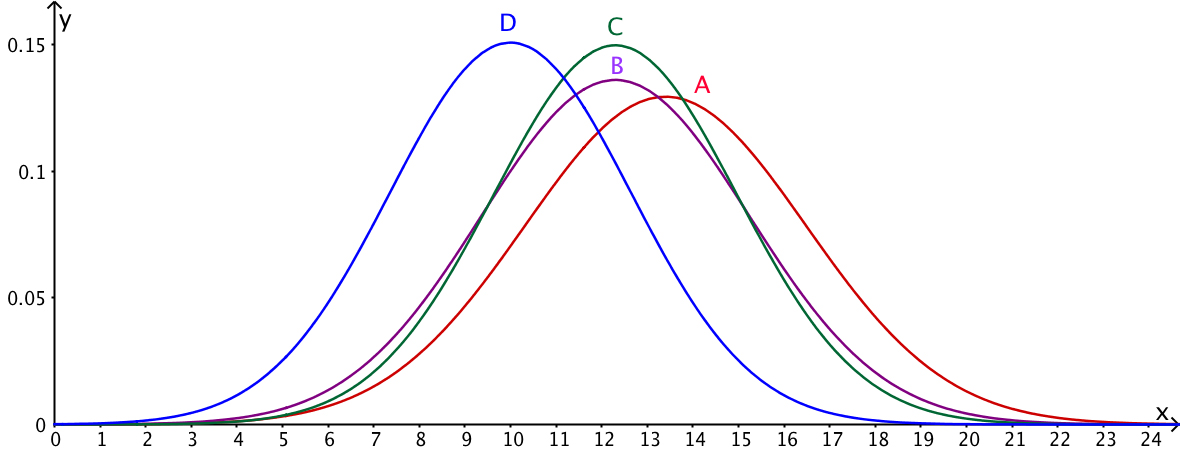
In unserem Beispiel ist der Fisherquotient 3.31. Die Streuung der Mittelwerte scheint also eine Rolle zu spielen. Ist dies aber hinreichend, um die Nullhypothese zu widerlegen?
Darüber gibt die Fisher-Verteilung Auskunft. Diese ist aber abhängig von der Stichprobengrösse, genauer von den sogenannten Freiheitsgraden (den Nennern) von MSB und MSE.
MSB hat in unserem Beispiel k-1=3 Freiheitsgrade (die Varianzformel hat Nenner 3).
MSE ist ein Mittelwert von k Varianzen mit je (n-1) Freiheitsgraden, hat somit
k⋅(n-1) = k⋅n - k = N - k Freiheitsgrade, in unserem Beispiel also 48.
Anschaulich im Beispiel oben:
Jede der vier Gruppenvarianzen hat in der Varianzformel Nenner n-1=12; wir addieren diese Varianzen (-> immer noch Nenner 12) und dividieren bei der Mittelwertsbildung durch k=4; so entsteht Nenner k⋅(n-1)=48.
Die kritische Grenze für die Fisher-Verteilung von MSB : MSE in Abhängigkeit des Zählerfreiheitsgrades (Freiheitsgrad von MSB; im Beispiel Wert 3) und des Nennerfreiheitsgrades (Freiheitsgrad von MSE; im Beispiel Wert 48) kann in einer Tabelle oder in einem Online-Rechner festgestellt werden.
In unserem Beispiel schneidet der Wert 3.31 vom rechten Teil der 3-48-Fisher-Verteilung ca. 2.8% ab, d.h. unter der Voraussetzung der Nullhypothese wäre ein Wert von 3.31 ziemlich unwahrscheinlich; wir verwerfen auf dem 5%-Signifikanzniveau die Nullhypothese und konstatieren: Mindestens zwei Trainingsmethoden unterscheiden sich bei diesem Signifikanzniveau in der Wirksamkeit. Welche wird jedoch nicht gesagt, und auch über die "Richtung" (besser oder schlechter) gibt es keine Auskunft: Der Test ist zweiseitig.
Auf dem 1%-Signifikanzniveau muss jedoch die Nullhypothese beibehalten werden. Mindestens zwei Methoden unterscheiden sich also signifikant (5%-Niveau), jedoch nicht hochsignifikant (1%-Niveau).
Bild rechts: Fisher-Verteilung unseres Beispiels.
Geogebra-Modell für die F-Verteilung bei verschiedenen Zähler- und Nennerfreiheitsgraden hier.

Anmerkung
Warum können nicht einfach je zwei Trainingsgruppen miteinander verglichen werden? Bei vier Gruppen A, B, C, D ergäbe dies sechs paarweise t-Tests auf Gleichheit der Mittelwerte, nämlich A-B, A-C, A-D, B-C, B-D, C-D.
Antwort: Bei jedem der 6 Tests auf Signifikanzniveau 5% ist die Wahrscheinlichkeit eines Fehlers erster Art 0.05. Wie gross ist dann die Wahrscheinlichkeit, in 6 Tests mindestens ein Mal einen solchen Fehler zu begehen?
Lösung: Wir arbeiten mit der Gegenwahrscheinlichkeit, also der Wahrscheinlichkeit, in 6 Tests keinen Fehler zu begehen. Diese Wahrscheinlichkeit beträgt 0.956 = 73.5%. Die gesuchte Wahrscheinlichkeit ist also 26.6% = Wahrscheinlichkeit mindestens eines Fehlers. Dies ist ein zu hoher Wert. Wir sprechen von einer Alpha-Fehler-Inflation.
Es gibt paarweise Post-hoc-Tests, die diese Schwierigkeit angehen.
Vergleichen wir in unserem Beispiel etwa D-A, D-B und D-C je paarweise (3 Tests), so müssen wir wegen der α-Fehler-Inflation für jeden Test das Signifikanzniveau senken. Nehmen wir hier statt 5% den Wert 1.7%. Bei 3 Tests ist dann die Wahrscheinlichkeit, mindestens ein Mal einen Fehler 1. Art zu begehen etwa 5%. Wir finden auf diesem Signifikanzniveau, dass sich lediglich D und A signifikant unterscheiden.
Der t-Test für den Vergleich der Mittelwerte von zwei unabhängigen Stichproben ist äquivalent zur einfaktoriellen Varianzanalyse mit k = 2, d.h. Zählerfreiheitsgrad 1.
Wir wiederholen das Beispiel von "Wahrscheinlichkeit 03; t-Test, Beispiel 2":
Man will die Wirksamkeit einer bestimmten Substanz auf die Konzentrationsfähigkeit einer Person testen.
Dazu testen wir in einem Doppelblindversuch je 15 Personen.
Gruppe S erhält während einer definierten Zeitspanne die Substanz, Gruppe P ein Placebo-Produkt. (In einem Doppelblindversuch wissen weder die Probanden noch die Versuchsleiter, wer zur Placebo-Gruppe gehört.)
Anschliessend wird ein geeichter Konzentrationstest durchgeführt, dessen Resultat eine "Konzentrationszahl" ist.
Wir vergleichen die Mittelwerte dieser Konzentrationszahlen für jede Gruppe separat und finden folgende Ergebnisse:
n1 = 15, ![]() = 112.0, s1= 14 (Gruppe, welche die Substanz erhielt).
= 112.0, s1= 14 (Gruppe, welche die Substanz erhielt).
n2 = 15, ![]() = 100.5, s2= 16 (Placebo-Gruppe).
= 100.5, s2= 16 (Placebo-Gruppe).
Prüfgrösse t-Test: t = 2.09495
kritische Grenze zum 5%-Signifikanzniveau, zweiseitig: t* = 2.04841
(t-Verteilungsrechner hier)
Der kritische Wert wird auf dem 5%-Niveau leicht überschritten: Ablehnung der Nullhypothese "keine Wirkung". Auf dem 1%-Niveau würde allerdings die Nullhypothese beibehalten.
Nun führen wir denselben Test varianzanalytisch durch:
| Gruppe | Mittelwert der Gruppe | Varianz |
| S ("Substanz") | 112 | 196 |
| P ("Placebo") | 100.5 | 256 |
| Mittelwert der Spalten | 106.25 | 226 |
Varianz der Gruppenmittelwerte: 66.125 (Varianzformel mit Nenner 1).
n = 15 Personen in jeder Gruppe. k = 2 (Gruppe S bzw. P). N = 30.
MSE = 226
MSB = 15⋅66.125 = 991.875
F = MSB : MSE = 4.38883 = Prüfgrösse.
Zählerfreiheitsgrad: 1; Nennerfreiheitsgrad: 28
Kritischer F-Wert für 5%-Niveau: 4.19597

Vergleich mit dem t-Test: Man sieht, dass die Werte der Varianzanalyse die quadrierten Werte des t-Tests sind, sowohl für die Prüfgrösse als auch für die kritische Grösse.
Somit sind beide Tests äquivalent und liefern dieselben Resultate.
Ein schönes Ergebnis, beruhen doch die beiden Tests auf verschiedenen Verteilungen (t-Verteilung; F-Verteilung mit Zählerfreiheitsgrad 1).
Der Vergleich zeigt ebenfalls, dass die Varianzanalyse zweiseitig testet, obwohl in der F-Verteilung nur rechts Fläche abgeschnitten wird, während beim t-Test in der t-Verteilung links und rechts je 2.5% abgeschnitten wurden.

Mit Excel kann das Einführungsbeispiel (4 Gruppen à 13 Personen; Beweglichkeitstrainings A, B, C, D) simuliert werden. Dadurch wird das Entstehen der Fisher-Verteilung etwas anschaulicher.
Zunächst konstruieren wir eine Grundpopulation mit Mittelwert 12 und Varianz 8 für die Beweglichkeitspunkte im Beweglichkeitstest (s. Einführungsbeispiel):
Wir würfeln mit 6 gewöhnlichen Spielwürfeln und bilden die Augensumme X.
Unser Resultat "Beweglichkeitspunkte" errechnen wir mittels
Z = (X-21)√8 /4.183+12 = 0.676*(X - 21) + 12.
Dies ergibt, genügend oft wiederholt, eine Population mit Mittelwert 12 und Varianz 8, also ungefähr das, was wir in unserem Einführungsbeispiel hatten. Wir gehen aus von der Nullhypothese, programmieren somit keinerlei Trainingseffekte ein.
Die so konstruierte Population ist natürlich immer noch stark vereinfacht im Vergleich zu einer wirklichen menschlichen Population, sind doch mit 6 Würfeln lediglich 31 verschiedene Augensummenwerte möglich und die Verteilung ist überhaupt keine perfekte Normalverteilung.
Die Excel-Felder B1 bis G52 (s. Bild links) erzeugen die Würfelzahlen via Befehl
GANZZAHL(ZUFALLSZAHL()*6+1).
In der H-Spalte wird jeweils die Summe der 6 Augenzahlen einer Zeile berechnet:
H1= SUMME(B1;G1), usw.
Die I-Spalte errechnet die Z-Werte gemäss obiger Formel: I1=0.676*(H1-21)+12, usw.
(Es sind "Beweglichkeitswerte" zwischen 2 und 22 möglich.)
Die 4 Trainingsgruppen A bis D sind farblich voneinander abgegrenzt.
J12 = MITTELWERT(I1;I13), J13=VARIANZA(I1;I13), usw.
[gruppenweise Mittelwerte (J12;J25;J38;J51) bzw. Varianzen (J13;J26;J39;J52)]
K34 = MITTELWERT(J13;J26;J39;J52) = MSE-Wert = Mittelwert der Gruppenvarianzen.
M34 = 13*VARIANZA(J12;J25;J38;J51) = MSB-Wert = 13-mal Varianz der Gruppenmittelwerte.
O34 = M34/K34 = F-Wert = MSB / MSE.
Q34 erzeugt eine Klasseneinteilung mit Säulenbreite 0.4. Die Klassenmitte ergibt sich folgendermassen: Q34=VRUNDEN(O34+0.2;0.4)-0.2. Durch diese Klassenbildung kann ein Histogramm gebildet werden.
Via ⌘= wird nun das Excelblatt immer wieder ausgewertet, z.B. 200-mal. Die in die Säulenklassen eingeteilten F-Werte werden notiert und als Histogramm dargestellt.
Man sieht: Hohe Werte kommen selten vor, denn das Excelblatt ist ja für die Nullhypothese (kein Trainingseinfluss) programmiert. Am häufigsten werden Werte zwischen ca. 0.2 und 1 sein. Dies stimmt ungefähr mit der theoretischen Fisherverteilung (s. Vergleich unten) überein.
Bild rechts:
Histogramm mit 200 Zufallsauswertungen. (200 erneute Auswertungen ergäben ein leicht anderes Histogramm.)
Im Histogramm gibt die Säulenfläche die prozentuale Häufigkeit der F-Werte an, welche in diese Säulenklasse fallen. Die gesamte Histogrammfläche ist gleich 1 oder 100%.
Die Säulenbreite ist 0.4, d.h. wir klassieren die F-Werte in folgende Säulenklassen: [0;0.4), [0.4;0.8), [0.8;1.2), usw.
x-Achse: F-Wert.
Lesebeispiel: Säule 1:
0.6625*0.4 = 0.265 = 26.5%, das heisst: 26.5% der 200 Auswertungen (das sind 53 Auswertungen) ergaben einen F-Wert zwischen 0 und 0.4, d.h. Säule 1 nimmt 26.5% der gesamten Histogrammfläche ein.
Zum Vergleich ist die theoretische F-Dichteverteilung rot eingezeichnet. Wäre die Zahl der Auswertungen viel höher als 200, so näherte sich die Histogrammform (mit schmaleren Säulenklassen) noch besser dem rot gezeichneten Graphen an.
Auf dem 5%-Signifikanzniveau würden wir ab einem F-Wert von ca. 2.8 die Nullhypothese (hier fälschlicherweise) verwerfen. In unseren 200 Auswertungen kam dies 15-mal vor, also etwas öfter als theoretisch vorausgesagt. Auf dem 1%-Niveau läge die kritische F-Grenze bei ca. 4.2; in unseren 200 Auswertungen wurde der Wert 4 nie überschritten (dieser Fall könnte aber durchaus -selten- eintreten).

Unten: Langsame Entstehung einer Normalverteilung beim Würfeln mit n Würfeln und Bilden der Augensumme. Erst ab ca. n = 25 kann man von einer guten Normalverteilungs-Näherung sprechen.

Bildquelle: https://www.rechner.club/wahrscheinlichkeit/wuerfelsumme-tabelle
Für die Simulation im Bild rechts wurden pro Wurf 25 Würfel geworfen, welche zur Augensumme X addiert und zu einer "Beweglichkeitspunktezahl" verrechnet wurden; Punktezahl = 0.33(X-87.5)+12. (Diese Formel könnte theoretisch auch negative Punktezahlen liefern; die Wahrscheinlichkeit dafür ist jedoch praktisch 0, nämlich etwa 0.001%.)
Wir erhalten auf diese Weise für die Grundpopulation unseres Beispiels eine recht gute Normalverteilungsnäherung mit Varianz 8 und Mittelwert 12.
Hier eine Simulation mit 1000 Auswertungen und Balkenbreite 0.2.
Das Histogramm passt bereits recht gut in die Fläche unter der roten F-Kurve.

Hier nochmals das Beispiel "Beweglichkeitstraining nach 4 Trainingsmethoden":
4 Gruppen à 13 Personen.
Nehmen wir an, wir hätten folgende Resultate erhalten:

Wenn wir nur die Zähler der beteiligten Varianzen betrachten (wir nennen sie "Quadratsummen"), finden wir bezogen auf unser Beispiel folgendes:
48⋅MSE + 3⋅MSB = 51⋅Gesamtvarianz.
(Zudem: 48 + 3 = 51.)
Dieser Zusammenhang zwischen den Zählern (den Quadratsummen) gilt allgemein.
SSE: sum of squares of errors: Quadratsumme, die aufgrund von Zufälligkeiten bei den Gruppenbeteiligten zustande kommt (unterschiedliche Grundbeweglichkeit, individuelle Motivation, Tagesform, usw.).
Hier fliesst also keine Streuung der Gruppenmittelwerte ein (und damit auch kein allfälliger Behandlungseffekt).
SSB: sum of squares between groups: Wir denken uns in den farbigen Spalten links alle Werte einer Gruppe durch den Gruppenmittelwert ersetzt, also z.B. in Gruppe A durch 13.23.
Wir betrachten den Gesamtmittelwert GM = 12.13 und bilden folgende Quadratsumme:
13⋅(13.23-12.13)2 + 13⋅(11.69-12.13)2 + 13⋅(12.77-12.13)2 + 13⋅(10.85-12.13)2.
Vorsicht Rundungsfehler!
In diese Summe fliessen zwei Effekte ein: Ein "Stichprobeneffekt" (der Stichprobenmittelwert weicht bei den meisten Stichproben vom Populationsmittelwert ab; dies ist ein natürlicher Mittelwert-Streueffekt bei der Ziehung von Stichproben)
und ein allfälliger Behandlungseffekt, der die Gruppenmittelwerte zusätzlich streuen lässt.
Sei SST = sum of squares total = Zähler der Gesamtvarianz.
Dann gilt: SSE + SSB = SST.
Bemerkung zum Beispiel oben:
Zunächst eine Zusammenfassung der Werte:
| Freiheits-grad f | Quadrat- |
QS / f | F = MSB/MSE |
p | |
| gruppeneinteilungs- bedingt (Stichproben- und Behandlungseffekt; Streuung zwischen den Gruppen) |
3 | SSB = 44.98 | MSB = 14.99 | 3.475 | 0.023 |
| individuell bedingt (Streuung innerhalb der Gruppen) |
48 | SSE = 207.08 | MSE = 4.314 | ||
| total | 51 | SST = 252.06 | s2 = 4.942 |
Beim F-Wert 3.475 im obigen Beispiel werden rechts dieses Wertes in der Verteilung 2.3% Fläche abgeschnitten.
Auf dem 5%-Signifikanzniveau befinden wir uns somit im Ablehnungsbereich der Nullhypothese "keine Treatmentwirkung".
Auf dem 1%-Niveau sind wir noch im Annahmebereich der Nullhypothese.
Obiges Beispiel entstand via Excel-Simulation, die keinen Treatmenteinfluss einprogrammiert hat, also unter Gültigkeit der Nullhypothese. Es ist ein seltener Fall eines Fehlers 1. Art (irrtümliche Verwerfung der Nullhypothese). Die Wahrscheinlichkeit, dass F bei Gültigkeit der Nullhypothese ≥3.475 ist, beträgt rund 2.3%, ist also selten.
In unserem Fall besteht z.B. Stichprobe D (Gruppe D) zufälligerweise aus lauter eher unbeweglichen Personen (Mittelwert eher tief, Varianz eher gering). Eine solch unglückliche Zufallsauswahl kann in seltenen Fällen vorkommen. (Einen systematischen Fehler bei der Gruppenbildung können wir hier ausschliessen - auch dies könnte jedoch bei einem dilettantisch geplanten Experiment vorkommen.)
MSB wird wegen Gruppe D aufgrund der erhöhten Streuung der Gruppenmittelwerte relativ hoch und MSE aufgrund des relativ tiefen Mittelwerts der Gruppenvarianzen eher tief ausfallen, obwohl kein Behandlungseffekt mitspielt. Dies führt dann zu einem hohen F-Wert und einem Fehler 1. Art.
Wollen wir ein solches Risiko verkleinern, wählen wir besser ein 1%-Signifikanzniveau; dieses wird bei medizinischen Forschungen auch oft gewählt.
Eine unglückliche Zufallsauswahl wie sie in Gruppe D auftrat, kann natürlich auch die Unabhängigkeit der Ergebnisse im Beweglichkeitstest beeinträchtigen: Es besteht die Gefahr, dass man sich in dieser Gruppe generell weniger anstrengt (Querbeeinflussungen). Damit wäre eine der Grundvoraussetzungen für ANOVA (Unabhängigkeit der Ergebniswerte) verletzt.
Beweis von SSE + SSB = SST
Wir benötigen den sogenannten Steinerschen Verschiebungssatz als Hilfssatz für den Beweis:

q.e.d.
Damit lässt sich nun die Behauptung SSE +SSB = SST leicht beweisen (Spalte rechts):

Die Komponenten der einzelnen Messwerte

Wir wählen erneut unser Beispiel: k Trainingsgruppen à n Personen (gleiche Personenzahl pro Gruppe). yi j = j-ter Messwert in der i-ten Gruppe.
μ= Mittelwert aller Messwerte; μi = Mittelwert der i-ten Gruppe;
εi j = individuelle Abweichung vom Gruppenmittelwert = "Versuchsfehler".
Wir finden: yi j = μ + τi + εi j . Die Summe der τi über alle Gruppen ist gleich 0.
Es ist (yi j - μ) = (μi - μ) + (yi j - μi).
Dieses Schema entspricht der Darstellung auf www.methodenberatung.uzh.ch.