Logarithmen, abgegriffene Buchseiten und frisierte Bilanzen: Das Gesetz von Benford

Quelle: http://de.wikipedia.org/wiki/Logarithmentafel

1881 bemerkte der amerikanische Astronom Simon Newcomb, dass in zahlreichen Logarithmentafeln die ersten Seiten deutlich stärker abgegriffen waren als die hinteren. Das erschien ihm seltsam. Auf den ersten Seiten musste man stets nachschlagen, wenn man mit Zahlen rechnete, deren erste von Null verschiedene Ziffer eine 1 war,
z.B.  147.28;  0.0145;  0.18.

Dass die ersten Seiten abgegriffener waren, konnte nur bedeuten, dass Zahlen, die mit einer 1 begannen, häufiger vorkamen als etwa Zahlen, die mit einer 9 begannen. Konnte das tatsächlich sein?

Newcombs Beobachtung geriet wieder in Vergessenheit, bis 1938 ein amerikanischer Elektroingenieur, Frank Benford, das Phänomen erneut entdeckte. Er analysierte etwa 20'000 Zahlen, die auf verschiedenste Weise zusammengekommen waren: Einwohnerzahlen amerikanischer Städte, physikalische Konstanten in Formelsammlungen, Zeitungsauflagen, Entwässerungsgebiete von Flüssen, Zahlen aus der Zeitschrift "Reader's Digest", usw. Tatsächlich: Rund 30% dieser Zahlen hatten eine 1 als führende Ziffer, ca. 17% eine 2 und ca. 12% eine 3. Das waren bereits 60% der untersuchten Zahlen!

Das Phänomen wurde genauer untersucht.
Nicht alle Zahlenlisten folgen diesem Benfordschen Gesetz, aber doch sehr viele, z.B. auch Daten in Bilanzen und Rechnungsabschlüssen.

Die einfachste Form des Benfordschen Gesetzes betrifft die erste Ziffer ≠ 0 einer Zahl:
Die Wahrscheinlichkeit, dass diese erste Ziffer den Wert d hat, beträgt

Beim Fälschen von Daten wird nun die gewissermassen "natürlicherweise" entstandene Benford-Ordnung gestört. Deshalb ist es möglich, mit Hilfe des Benford-Gesetzes z.B. Bilanzen zu prüfen. So wiesen etwa die Zahlen des griechischen Staatshaushaltes der jüngeren Gegenwart wesentliche Abweichungen vom Benfordschen Gesetz auf, was auf Manipulationen hindeutet. Auch die belgische Bilanz fällt diesbezüglich schlecht aus.

Benfords Gesetz wird heute tatsächlich zur Überprüfung von Zahlenmanipulationen eingesetzt.
Das Manipulieren von Bilanzen wird damit sehr schwierig. Das Gesetz der ersten Ziffer (siehe Formel oben) kann man ja noch leicht berücksichtigen. Doch eine Bilanz so zu fälschen, dass auch alle Gesetze für die 2., 3., ... Ziffer und für Gruppen von Ziffern gleichzeitig erfüllt sind, ist ein fast unmögliches Unterfangen, obwohl die Kontroll-Formeln offen vorliegen.

Die Mathematiker haben in den letzten 30 Jahren recht konkret eingrenzen können, welche Arten von Zahlensammlungen benford-verträglich sind und welche nicht. Es müssen Sammlungen sein, die sehr grosse und sehr kleine Werte umfassen und deren Zahlen durch möglichst viele, voneinander unabhängige Einflüsse entstanden sind. Dass Bilanzen zu den benford-verträglichen Zahlen-Sammlungen gehören, ist Pech für Erzeuger "kreativer" Abschlüsse.

So stand hier eine skurrile Beobachtung an verschmutzten Logarithmentafeln am Anfang einer Entwicklung, die schliesslich zu logarithmischen Gesetzen führte, mit deren Hilfe man Hinweise auf Bilanzmanipulationen erhalten kann.

Setzt man für d der Reihe nach die Ziffern 1 bis 9 ein, findet man folgende Wahrscheinlichkeiten, dass die Ziffer d die führende Ziffer einer Zahl ist:

Ziffer 1 führend: 30.1%
Ziffer 2 führend: 17.6%
Ziffer 3 führend: 12.5%
Ziffer 4 führend:   9.7%
Ziffer 5 führend:   7.9%
Ziffer 6 führend:   6.7%
Ziffer 7 führend:   5.8%
Ziffer 8 führend:   5.1%
Ziffer 9 führend:   4.6%

Rechenbeispiel für d = 3:

Wahrscheinlichkeit, dass 3 die führende Ziffer ist = lg(4/3) ≈ 0.125 ≈ 12.5%.

Benfords Gesetz der ersten Ziffer wurde erweitert. Man hat heute Formeln für die Wahrscheinlichkeiten der 2., 3., 4., ... Ziffer, ja sogar für Gruppen von Ziffern. Man kann also auch die Wahrscheinlichkeit angeben, mit der etwa in einer Zahl die Gruppe "1 3 4" an 2. Stelle vorkommt, also etwa in 7 "1 3 4" 5. 8 3 2.

Die Nachfolger der alten Logarithmentafeln sind Computertastaturen:

In obiger Fotografie einer Computertastatur wird der Staub, der sich auf den Tasten "eingebrannt" hat, mittels Bildbearbeitung stark übertrieben dargestellt (massive Kontrasterhöhung). Man erkennt deutlich, dass die Tasten 1 und 2 am wenigsten "eingebrannten" Staub enthalten; offenbar werden diese Tasten viel öfter benutzt als die übrigen Zifferntasten und dadurch dauernd gereinigt: das moderne Analogon zu Newcombs Beobachtung an Logarithmentafeln. Oder wie Prof. Thomas Jech es ausdrückte: "When the '1' key on my old computer gave out I was not surprised."

Infos z.T. aus: www.educ.ethz.ch/unt/um/mathe/ana/benford
Schlusszitat aus: www. math.psu.edu/jech/preprints/digits.pdf

Es gibt Zahlenfolgen, die -wenn sie sehr weit aufgeführt werden- in der Verteilung der führenden Ziffern das Benford-Gesetz erfüllen, es gibt aber auch Folgen, bei denen dies nicht der Fall ist.

Beispiele für benford-verträgliche Folgen:

• Geometrische Folgen (qⁿ) mit lg(q) irrational. Als Beispiel können wir etwa die Folge (2ⁿ) der Zweierpotenzen betrachten: 1  2  4  8  16  32  64  ...
• Folge der Fibonacci-Zahlen 1  1  2  3  5  8  13  21  34  55  ...
• Folge der Fakultäten 1, 2, 6, 24, 120, 720, ...

Beispiele für nicht-benford-verträgliche Folgen:

• Folge der Primzahlen
• arithmetische Folgen
  

Beispiel: Folge der Zweierpotenzen

1  2  4  8  16  32  64  128  256  512  1024  2048  4096  8192  16384  ...

Wir interessieren uns hier nur für die erste Ziffer. Deshalb können wir alle Zahlen der Folge reduzieren und zwar wie folgt:

1  2  4  8  1.6  3.2  6.4  1.28  2.56  5.12  1.024  2.048  4.096  8.192  1.6384  ...

Wir erhalten dann lauter Zahlen im Intervall [1;10[. Wir ignorieren also die fehlenden Zehnerpotenzen; die führenden Ziffern bleiben ja bei dieser Reduktion dieselben. Bereits hier sieht man, dass die führende Ziffer 1 in fünf der oben aufgeführten Zahlen vorkommt. Die 8 tritt nur zwei Mal auf, die 9 wird erst als führende Ziffer von 2⁵³ die Bühne betreten.

Je länger diese Folge aufgeführt wird, desto mehr wird sich die Verteilung der führenden Ziffern dem Benford-Gesetz annähern (s. blauer Kasten links). Dies soll im Folgenden heuristisch "begründet" werden.

Zunächst einige sehr pauschale Bemerkungen:

• Führen wir die Folge immer weiter (zusammen mit unserer Reduktion), so "regnet" es immer mehr Zahlen ins Intervall [1; 10[ hinein.
• Diese Zahlen sind nicht gleichmässig verteilt; im Bereich der Eins und der Zwei finden sich deutlich mehr Zahlen als etwa im Bereich der Acht oder der Neun. Die Verteilung ist nicht homogen.
• Es gilt immer a_n+1 = a_n ⋅ 2

Indem wir von den Zahlen unserer geometrischen Folge zu den Logarithmen (wir wählen die Zehnerlogarithmen) übergehen, erhalten wir eine arithmetische Folge, denn es gilt:

• lg(a_n+1) = lg(a_n) + lg(2).
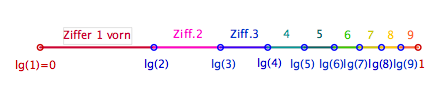
• Durch das Logarithmieren mit dem Zehnerlogarithmus wird das Intervall [1; 10[ ins Intervall [lg(1) ; lg(10)[ = [0 ; 1[ transformiert (s. Bild links).
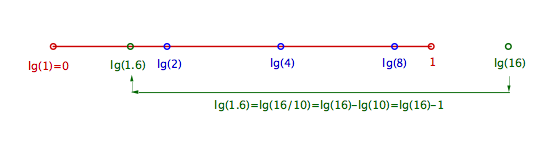
• Die Logarithmen unserer reduzierten Folgeglieder werden jetzt also ins Intervall [0 ; 1[ geworfen, und zwar entsteht die nächstfolgende Zahl immer durch Addition von lg(2) aus der Vorgängerzahl. Wir sehen im Bild links die Folge lg(1), lg(2), lg(4), lg(8). Mit lg(16) wird das Intervall [0 ;1[ überschritten, doch durch die Reduktion auf lg(1.6) = lg(16) - 1 gelangt der nächste Punkt wieder "von links her" ins Intervall hinein. So verbleiben alle entstehenden Punkte im Intervall [0 ; 1[.
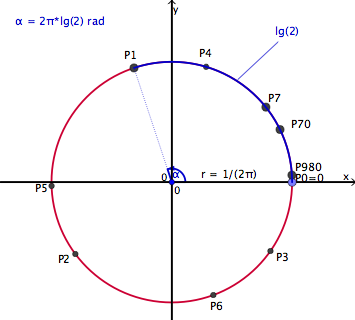
• Wir können die Sache noch anschaulicher gestalten, indem wir die Einheitsstrecke [0 ;1[ zu einem Kreis mit Umfang 1 biegen (Bild links unten): Wir starten mit P₀ = 0 auf der x-Achse. Die Punkte P₀ = 0, P₁ = lg(2), P₂ = lg(4), usw. entstehen jetzt laufend auf dieser Kreislinie. Von Punkt zu Punkt wird stets ein Bogenstück der Länge lg(2) addiert (vgl. blaues Stück von P₀ nach P₁ im Bild links).
• Da lg(2) irrational ist (und damit auch der Drehwinkel α = 2π⋅lg(2) rad ≈108.4...° irrational ist), entstehen im Laufe vieler hintereinander ausgeführter Drehungen α ständig neue Punkte; nie wird ein alter Punkt getroffen (dies wäre der Fall, wenn der Drehwinkel α rational wäre).
• Wir sehen, dass mit P₇, P₇₀, P₉₈₀, usw. Punkte entstehen, deren zugehöriger Winkel zur x-Achse immer kleiner wird. Die Punktreihe P₉₈₀ , P_2⋅980 , P _3⋅980, usw. erzeugt bereits eine sehr feinmaschige Punktreihe auf dem Kreis (zugehöriger Drehwinkel ca. 3.4...°). Diese Feinmaschigkeit können wir beliebig steigern.
• Zudem könnten wir mit unserer Drehung α bei jedem Punkt starten, womit sich von jedem Punkt ausgehend die gleiche Punkteverteilung auf der Kreislinie ergibt. Die Vermutung liegt nahe, dass die Punkteverteilung bei wachsender Anzahl Punkte homogen wird: Die Punkte verteilen sich gleichmässig auf der Kreislinie und ballen sich nicht in einzelnen Bereichen.
• In komplexer Exponentialschreibweise gilt übrigens für den Punkt P_k :
  P_k = (1/2π)⋅e^{i⋅2π⋅lg(2)⋅k}.
• Fassen wir die Punkte P_k als komplexe Zahlen auf, so gilt genau bei homogener Verteilung
  
  Anschaulich: Der Schwerpunkt der Punkte P₀ bis P_N (aufgefasst als Massenpunkte mit Masse 1) nähert sich mit wachsendem N dem Punkt 0 an.

Beispiel: Der Bruchteil der türkisfarbenen Strecke gemessen an der ganzen Einheitsstrecke ist die Wahrscheinlichkeit, dass die führende Ziffer einer Zahl der Folge (2ⁿ) - allgemein auch der Folge (qⁿ) mit lg(q) irrational - eine 4 ist. Die Länge der türkisfarbenen Strecke ist gleich lg(5) - lg(4) = lg(5/4).

Schlussresultat

• Die Punkte P_k verteilen sich bei sehr grosser Anzahl homogen auf dem Kreis mit Umfang 1. Oder gleichbedeutend: Die Zehnerlogarithmen lg(a_k) der reduzierten Folgeglieder a_k = 2^k verteilen sich homogen auf der Einheitsstrecke [0 ; 1 [.
• Die Zahlen a_k mit führender Ziffer 1 (1.000... bis 1.999...) gehen beim Logarithmieren auf das Streckenstück lg(1.000...) bis lg(1.999...), diejenigen mit führender Ziffer 2 auf das Stück lg(2.000...) bis (2.999...), usw. Links sind diese Stücke in verschiedenen Farben dargestellt.
• Bei homogener Verteilung der Punkte ergibt sich als Wahrscheinlichkeit, dass die führende Ziffer = d ist somit der Wert [lg(d+1) - lg(d)] / 1 = lg(d+1) - lg(d) oder
  lg[(d + 1) / d]. Dies ergibt sich aus der Wahrscheinlichkeitsformel "günstige Fälle dividiert durch mögliche Fälle", die wir anwenden dürfen, weil wir gezeigt haben, dass die Punkteverteilung im Grenzfall unendlich vieler Punkte homogen ist.

Aufgabe:
Wie gross ist die Wahrscheinlichkeit, dass die zweite Ziffer einer Benford-Folge eine 1 ist?

Lösung:
In Frage kommen die Anfangspakete 11, 21, 31, 41, 51, 61, 71, 81, 91.
Wir addieren die entsprechenden Wahrscheinlichkeiten.

p("zweite Ziffer = 1") = lg(12/11) + lg(22/21) + lg(32/31) + ... + lg(92/91) ≈0.1139 ≈11.39%.
Analog lässt sich die Wahrscheinlichkeit für Ziffern und Ziffernpakete an beliebiger Stelle einer Zahl berechnen.

Aufgabe:
Wie gross ist die Wahrscheinlichkeit, dass die zweite Ziffer einer Benford-Folge eine 1 ist, wenn man weiss, dass die erste Ziffer eine 1 ist? (Bedingte Wahrscheinlichkeit.)

Lösung:
p = #Günstige / # Mögliche = [lg(12)-lg(11)] / lg(2) ≈ 0.1255 ≈ 12.55%

Vergleicht man die Ergebnisse beider Aufgaben, bemerkt man überraschenderweise, dass die Wahrscheinlichkeit, dass die zweite Ziffer eine 1 ist davon abhängt, wie gross die erste Ziffer ist! Die erste Ziffer beeinflusst also die Wahrscheinlichkeit für das Auftreten der zweiten Ziffer.
Je weiter zwei Ziffern auseinanderliegen, desto geringer ist diese Bedingtheit.

Verallgemeinerung auf Zifferngruppen

Die Benford-Formel für die führenden Ziffern:
p("d = führende Ziffer") = lg(d + 1) - lg(d),
gilt auch für ganze Zifferngruppen am Anfang.
So beträgt die Wahrscheinlichkeit, dass eine Zahl einer Benford-Folge mit dem "Paket" 31 beginnt lg(32) - lg(31) = lg(32/31) ≈0.0138 ≈1.38%.

Skaleninvarianz

Habe ich etwa Flusslängen in km, welche dem Benford-Gesetz entsprechen, so werden auch die in englische Meilen umgerechneten Flusslängen dem Benford-Gesetz gehorchen. (Einige führende Ziffern 1 z.B. werden verschwinden, dafür andernorts neu auftauchen.)

Zusammenfassung

Die geometrische Folge (qⁿ) mit lg(q) irrational ist eine Benford-Folge.
Dass solche geometrische Folgen dem Benford-Gesetz gehorchen, lässt sich mathematisch plausibel nachvollziehen. Schwieriger ist eine plausible Erklärung mit andern Zahlendaten. Warum erfüllen etwa die Zahlen einer Sammlung physikalischer Konstanten das Benfordsche Zifferngesetz? Warum eine Sammlung von Flusslängen oder Grössen von Seen oder Ortschaften? Hier plausible Erklärungen zu finden, ist viel schwieriger und führt vielleicht sogar in naturphilosophische Sphären.

Benford's Law in der Physik

So wie Bilanzfälschungen via Abweichungen von Benfords Gesetz entdeckt werden können, ist es möglich, dass in physikalischen Bereichen, in denen Benfords Gesetz empirisch festgestellt wird plötzliche Abweichungen von diesem Gesetz darauf hindeuten, dass neue Einflüsse ins Spiel kommen, die man bisher noch nicht wahrgenommen hat. Die Benford-Verteilung wird deshalb auch für die Naturwissenschaft zunehmend interessant.

Eine ausgezeichnete Wikepedia-Seite zum Thema:
http://de.wikipedia.org/wiki/Benfordsches_Gesetz
Ferner:
http://www.benfordonline.net/